题目内容
设f(x)=
,又记f1(x)=f(x),fk+1(x)=f[fk(x)](k∈N+),则f2012(x)=( )
| 1+x |
| 1-x |
A、-
| ||
| B、x | ||
C、
| ||
D、
|
考点:函数的值
专题:函数的性质及应用
分析:求出函数的表达式,得到函数fn(x)的表达式具备周期性,利用函数的周期性即可得到结论.
解答:
解:∵f(x)=
,
∴f1(x)=f(x)=
,
f2(x)=f[f1(x)]=
=-
,
f3(x)=f[f2(x)]=
=
,
f4(x)=f[f3(x)]=
=x,
f5(x)=f[f4(x)]=f(x)=
,
…
∴fn(x)的表达式具备周期性,周期数是4,
∴f2012(x)=f4(x)=x,
故选:B
| 1+x |
| 1-x |
∴f1(x)=f(x)=
| 1+x |
| 1-x |
f2(x)=f[f1(x)]=
1+
| ||
1-
|
| 1 |
| x |
f3(x)=f[f2(x)]=
1-
| ||
1+
|
| x-1 |
| x+1 |
f4(x)=f[f3(x)]=
1+
| ||
1-
|
f5(x)=f[f4(x)]=f(x)=
| 1+x |
| 1-x |
…
∴fn(x)的表达式具备周期性,周期数是4,
∴f2012(x)=f4(x)=x,
故选:B
点评:本题主要考查函数解析式的求法,利用条件求出函数具备周期性是解决本题的关键.

练习册系列答案
相关题目
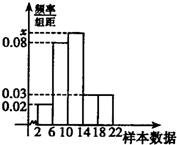 为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为( )
为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为( )| A、780 | B、660 |
| C、680 | D、460 |
定义域为R的函数f(x)=ax2+b|x|+c(a≠0)有两个单调区间,则实数a,b,c满足( )
| A、b2-4ac≥0且a>0 | ||
| B、b2-4ac≥0 | ||
C、-
| ||
D、-
|
已知实数x,y满足不等式组
,则2x-y的取值范围是( )
|
| A、[-1,3] |
| B、[-3,-1] |
| C、[-1,6] |
| D、[-6,1] |
已知等差数列{an}和{bn}的前n项和分别为Sn和Tn,且
=
,则
=( )
| Sn |
| Tn |
| 2n-1 |
| 2n+1 |
| a7 |
| b7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知sinα=-
,则cos(
-α)的值等于( )
| 1 |
| 3 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列统计图中,未丢失数据的统计图是( )
| A、茎叶图 | B、条形图 |
| C、折线图 | D、扇形图 |