题目内容
若不等式(a2-2a-3)x2-(a+2)x+
>0对于任何实数x都成立,求a的取值范围.
| 1 |
| 2 |
考点:一元二次不等式的应用
专题:计算题,不等式的解法及应用
分析:分别讨论:①当a2-2a-3=0即a=3或-1时,注意检验,②当a2-2a-3>0且△=(a+2)2-2(a2-2a-3)<0时两种情况解出即可.
解答:
解:①当a2-2a-3=0即a=3或-1时,-5x+
>0和-x+
>0,
对于一切实数x不都成立;
②当a2-2a-3>0且△=(a+2)2-2(a2-2a-3)<0时,对于任何实数x都成立,
即有a>3或a<-1且a>4+
或a<4-
,
解得,a>4+
或a<4-
,
则a的取值范围是:(-∞,4-
)∪(4+
,+∞).
| 1 |
| 2 |
| 1 |
| 2 |
对于一切实数x不都成立;
②当a2-2a-3>0且△=(a+2)2-2(a2-2a-3)<0时,对于任何实数x都成立,
即有a>3或a<-1且a>4+
| 26 |
| 26 |
解得,a>4+
| 26 |
| 26 |
则a的取值范围是:(-∞,4-
| 26 |
| 26 |
点评:本题考查不等式恒成立的条件,是基础题.要注意对二次项系数是否为0进行讨论.

练习册系列答案
相关题目
已知S=
•(sin
+sin
+sin
+…+sin
),则与S的值最接近的是( )
| π |
| 20000 |
| π |
| 20000 |
| 2π |
| 20000 |
| 3π |
| 20000 |
| 10000π |
| 20000 |
| A、0.99818 |
| B、0.9999 |
| C、1.0001 |
| D、2.0002 |
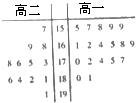 某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.
某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.