题目内容
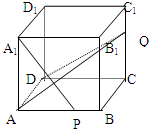 棱长是1的正方体,P、Q分别是棱AB、CC1的中点,
棱长是1的正方体,P、Q分别是棱AB、CC1的中点,(1)求证:A1P⊥平面AQD;
(2)求直线PQ与平面AQD所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)要证A1P⊥平面AQD,只需要证明A1P⊥AD,AR⊥A1P,利用三角形的全等可得AR⊥A1P,从而得证.
(2)求直线PQ与平面AQD所成角的正弦值,关键是寻找斜线PQ在平面内的射影,由(1)易得A1P与AR交于点S,连接SQ,则∠PQS即为PQ与平面AQD所成角,从而可解.
(2)求直线PQ与平面AQD所成角的正弦值,关键是寻找斜线PQ在平面内的射影,由(1)易得A1P与AR交于点S,连接SQ,则∠PQS即为PQ与平面AQD所成角,从而可解.
解答:
(1)证明:平面AQD与侧棱B1B的交点是R,则R是B1B的中点.
在正方形ABB1A1中,P是棱AB的中点,可得△A1AP≌△ABR,
所以AR⊥A1P,
又AD⊥平面ABB1A1,A1P?平面ABB1A1,得A1P⊥AD,AD∩AR=A,
所以A1P⊥平面AQD
(2)解:设A1P与AR交于点S,连接SQ,则∠PQS=θ即为PQ与平面AQD所成角.
在Rt△PQS中,|PS|=
,|PQ|=
,∴sinθ=
=
,
即直线PQ与平面AQD所成角的正弦值是
.
在正方形ABB1A1中,P是棱AB的中点,可得△A1AP≌△ABR,
所以AR⊥A1P,
又AD⊥平面ABB1A1,A1P?平面ABB1A1,得A1P⊥AD,AD∩AR=A,
所以A1P⊥平面AQD
(2)解:设A1P与AR交于点S,连接SQ,则∠PQS=θ即为PQ与平面AQD所成角.
在Rt△PQS中,|PS|=
| 4 | ||
3
|
| ||
| 3 |
| |PS| |
| |PQ| |
2
| ||
| 91 |
即直线PQ与平面AQD所成角的正弦值是
2
| ||
| 91 |
点评:本题的考点是直线与平面所成的角,主要考查线面垂直,考查线面角,关键是利用线面垂直的定义,寻找斜线在平面内的射影.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
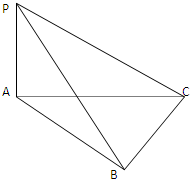 已知三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,BC=1,AC=
已知三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,BC=1,AC=