题目内容
已知函数f（x）=
，其中a＞0且a≠1．
（1）若f（f（-2））=
，求a的值；
（2）若f（x）在R上单调递减，求a的取值范围．
|
（1）若f（f（-2））=
| 1 |
| 9 |
（2）若f（x）在R上单调递减，求a的取值范围．
考点：指数函数单调性的应用
专题：函数的性质及应用
分析：（1）逐步代入，求得f（-2）=2，得f（f（-2））=f（2），计算即可．
（2）根据指数函数和一次函数的性质求出a相应的范围，注意若f（x）在R上单调递减，f（x）=（1-2a）x-4a+4的最小值大于等于f（x）=ax的最大值，继而求出a的范围．
（2）根据指数函数和一次函数的性质求出a相应的范围，注意若f（x）在R上单调递减，f（x）=（1-2a）x-4a+4的最小值大于等于f（x）=ax的最大值，继而求出a的范围．
解答：
解：（1）由f（-2）=-2（1-2a）-4a+4=2＞0，则f（f（-2））=f（2）=a2=
，
∵a＞0且a≠1．
∴a=
（2）当x≥0时，f（x）=ax，根据指数函数的性质，f（x）是减函数则0＜a＜1，
当x＜0时，f（x）=（1-2a）x-4a+4，根据一次函数的性质，f（x）是减函数则1-2a＜0，解得a＞
因为f（x）在R上单调递减-4a+4≥a0解得，a≤
综上所述a的取值范围（
，
]
| 1 |
| 9 |
∵a＞0且a≠1．
∴a=
| 1 |
| 3 |
（2）当x≥0时，f（x）=ax，根据指数函数的性质，f（x）是减函数则0＜a＜1，
当x＜0时，f（x）=（1-2a）x-4a+4，根据一次函数的性质，f（x）是减函数则1-2a＜0，解得a＞
| 1 |
| 2 |
因为f（x）在R上单调递减-4a+4≥a0解得，a≤
| 3 |
| 4 |
综上所述a的取值范围（
| 1 |
| 2 |
| 3 |
| 4 |
点评：本题主要考查了分段函数的单调性和函数值的求法，f（x）=（1-2a）x-4a+4的最小值大于等于f（x）=ax的最大值是本题的关键，属于基础题．
练习册系列答案
相关题目
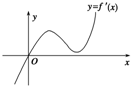定义在R上的函数f（x）满足f（4）=1，f′（x）为f（x）的导函数，已知函数y=f′（x）的图象如图所示．若两正数a，b满足f（2a+b）＜1，则
如图，四棱锥P-ABCD的底面是正方形，PA⊥底面ABCD，∠PDA=45°，点E为棱AB的中点，求证：平面PCE⊥平面PCD．
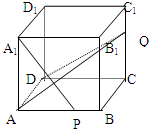棱长是1的正方体，P、Q分别是棱AB、CC1的中点，