题目内容
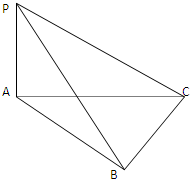 已知三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,BC=1,AC=
已知三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,BC=1,AC=| 2 |
(1)当PA=2时,求P(X=4)的值.
(2)当PA=1时,求变量X的分布列与期望.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(1)以CA为x轴,CB为y轴,建立空间直角坐标系,得到由任何二个顶点确定的向量的个数为
=15,其中X=4的有|
•
|,|
•
|,共2个,由此能求了P(X=4)=
.
(2)PA=1时,用列举法写出所有的15个向量的数量积的绝对值,得到X的取值为0,1,2,3,由此能求出变量X的分布列与期望.
| C | 2 6 |
| AP |
| PB |
| AP |
| PC |
| 2 |
| 15 |
(2)PA=1时,用列举法写出所有的15个向量的数量积的绝对值,得到X的取值为0,1,2,3,由此能求出变量X的分布列与期望.
解答:
解:(1)PA⊥平面ABC,∠ACB=90°,
BC=1,AC=
,PA=2,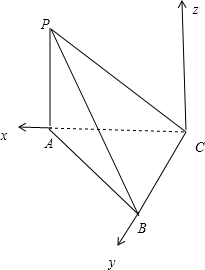
以CA为x轴,CB为y轴,建立如图所示的空间直角坐标系,
A(
,0,0),B(0,1,0),C(0,0,0),
P(
,0,2),
∴
=(-
,1,0),
=(-
,0,0),
=(0,0,2),
=(-
,1,-2),
=(0,1,0),
=(
,0,2),
由任何二个顶点确定的向量的个数为
=15,
其中X=4的有|
•
|,|
•
|,共2个,
∴P(X=4)=
.
(2)PA=1时,A(
,0,0),B(0,1,0),C(0,0,0),
P(
,0,1),
∴
=(-
,1,0),
=(-
,0,0),
=(0,0,1),
=(-
,1,-1),
=(0,1,0),
=(
,0,1),
|
•
|=2,|
•
|=0,|
•
|=3,|
•
|=1,|
•
|=2,
|
•
|=0,|
•
|=2,|
•
|=0,|
•
|=2,|
•
|=1,
|
•
|=0,|
•
|=1,|
•
|=1,|
•
|=3,|
•
|=0.
∴X的取值为0,1,2,3,
P(X=0)=
,P(X=1)=
,P(X=2)=
,P(X=3)=
,
∴X的分布列为:
EX=1×
+2×
+3×
=
.
BC=1,AC=
| 2 |

以CA为x轴,CB为y轴,建立如图所示的空间直角坐标系,
A(
| 2 |
P(
| 2 |
∴
| AB |
| 2 |
| AC |
| 2 |
| AP |
| PB |
| 2 |
| CB |
| CP |
| 2 |
由任何二个顶点确定的向量的个数为
| C | 2 6 |
其中X=4的有|
| AP |
| PB |
| AP |
| PC |
∴P(X=4)=
| 2 |
| 15 |
(2)PA=1时,A(
| 2 |
P(
| 2 |
∴
| AB |
| 2 |
| AC |
| 2 |
| AP |
| PB |
| 2 |
| CB |
| CP |
| 2 |
|
| AB |
| AC |
| AB |
| AP |
| AB |
| PB |
| AB |
| CB |
| AB |
| CP |
|
| AC |
| AP |
| AC |
| PB |
| AC |
| CB |
| AC |
| CP |
| AP |
| PB |
|
| AP |
| CB |
| AP |
| CP |
| PB |
| CB |
| PB |
| CP |
| CB |
| CP |
∴X的取值为0,1,2,3,
P(X=0)=
| 5 |
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
| 2 |
| 15 |
∴X的分布列为:
| P | 0 | 1 | 2 | 3 | ||||||||
X |
|
|
|
|
| 4 |
| 15 |
| 4 |
| 15 |
| 2 |
| 15 |
| 6 |
| 5 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E为棱AB的中点,求证:平面PCE⊥平面PCD.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E为棱AB的中点,求证:平面PCE⊥平面PCD.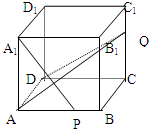 棱长是1的正方体,P、Q分别是棱AB、CC1的中点,
棱长是1的正方体,P、Q分别是棱AB、CC1的中点, 阅读如图所示程序:
阅读如图所示程序: