题目内容
函数f(x)=
的定义域为A,B={x|(x-2a)(x-a-1)<0}.
(1)求集合A;
(2)若B⊆A,求实数a的取值范围.
2-
|
(1)求集合A;
(2)若B⊆A,求实数a的取值范围.
考点:集合的包含关系判断及应用,函数的定义域及其求法
专题:函数的性质及应用,集合
分析:(1)要使函数f(x)=
有意义,则2-
≥0,且x+1≠0,解出即可;
(2)对2a与a+1的大小分类讨论,再利用B⊆A即可得出.
2-
|
| x+3 |
| x+1 |
(2)对2a与a+1的大小分类讨论,再利用B⊆A即可得出.
解答:
解:(1)要使函数f(x)=
有意义,
则2-
≥0,且x+1≠0,
化为(x+1)(x-1)≥0,x≠-1,
解得x<-1或x≥1.
∴函数f(x)的定义域为A=[1,+∞)∪(-∞,-1)
(2)当2a=a+1,即a=1时,B=Φ,满足B⊆A;
当2a>a+1,即a>1时,B=(a+1,2a).
∵B⊆A,∴a+1≥1或2a≤-1,解得a>1.
当2a<a+1,即a<1时,B=(2a,a+1).
∵B⊆A,∴2a≥1或a+1≤-1,解得
≤a<1或a≤-2.
综上可得:满足条件的a的取值范围为a≥
或a≤-2.
2-
|
则2-
| x+3 |
| x+1 |
化为(x+1)(x-1)≥0,x≠-1,
解得x<-1或x≥1.
∴函数f(x)的定义域为A=[1,+∞)∪(-∞,-1)
(2)当2a=a+1,即a=1时,B=Φ,满足B⊆A;
当2a>a+1,即a>1时,B=(a+1,2a).
∵B⊆A,∴a+1≥1或2a≤-1,解得a>1.
当2a<a+1,即a<1时,B=(2a,a+1).
∵B⊆A,∴2a≥1或a+1≤-1,解得
| 1 |
| 2 |
综上可得:满足条件的a的取值范围为a≥
| 1 |
| 2 |
点评:本题考查了求分式函数的定义域、分式不等式的解法、集合之间的关系,考查了分类讨论的思想方法,考查了计算能力,属于中档题.

练习册系列答案
相关题目


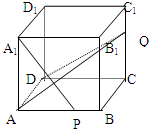 棱长是1的正方体,P、Q分别是棱AB、CC1的中点,
棱长是1的正方体,P、Q分别是棱AB、CC1的中点,