题目内容
正三棱锥P-ABC中,∠APB=∠BPC=∠CPA=90°,PA=PB=PC=a,AB的中点M,一小蜜蜂沿锥体侧面由M 爬到C点,最短路程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:多面体和旋转体表面上的最短距离问题
专题:空间位置关系与距离
分析:将侧面PAB,PBC,展开到一个平面,则△ABC中,CM为最短路线长.
解答:
解:由题意,将侧面PAB,PBC,展开到一个平面,

则△ABC中,AB⊥BC,BC=
a,BM=
a
∴CM=
=
a
即最短路线长是
a
故选:A

则△ABC中,AB⊥BC,BC=
| 2 |
| ||
| 2 |
∴CM=
(
|
| ||
| 2 |
即最短路线长是
| ||
| 2 |
故选:A
点评:本题考查多面体表面上的最短距离的计算,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若向量
,
,
的起点M和终点A,B,C互不重合,且无三点共线,则能使向量
,
,
成为空间一个基底的关系式是( )
| MA |
| MB |
| MC |
| MA |
| MB |
| MC |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
已知 PH⊥Rt△HEF所在的平面,且HE⊥EF,连接PE,PF,则图中直角三角形的个数是( )
| A、1 | B、2 | C、3 | D、4 |

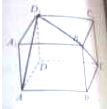 如图,已知ABCD-A1B1C1D1为正方体.
如图,已知ABCD-A1B1C1D1为正方体.