题目内容
已知对任意实数x,有f(-x)=-f(x),且当x>0时,有f′(x)>0,则当x<0时,有( )
| A、f'(x)≥0 |
| B、f'(x)>0 |
| C、f'(x)≤0 |
| D、f'(x)<0 |
考点:函数奇偶性的性质,利用导数研究函数的单调性
专题:函数的性质及应用
分析:先利用函数奇偶性的定义判断出f(x)的奇偶性;利用导数与函数的单调性的关系判断出函数在(0,+∞)
上的单调性,再据奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反得到f(x),g(x)在(-∞,0)的单调性,
再利用导数与函数的单调性的关系判断出导函数的符号.
上的单调性,再据奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反得到f(x),g(x)在(-∞,0)的单调性,
再利用导数与函数的单调性的关系判断出导函数的符号.
解答:
解:∵对任意实数x,有f(-x)=-f(x),
∴f(x)为奇函数;
∵x>0时,f′(x)>0,
∴f(x)在(0,+∞)上为增函数;
∴f(x)在(-∞,0)上为增函数;
∴f′(x)>0;
故选:B
∴f(x)为奇函数;
∵x>0时,f′(x)>0,
∴f(x)在(0,+∞)上为增函数;
∴f(x)在(-∞,0)上为增函数;
∴f′(x)>0;
故选:B
点评:导数的符号与函数单调性的关系为:导函数为正则函数单调递增;导函数为负,则函数单调递减;函数的奇偶性与单调性的关系:奇函数在对称区间的单调性相同,偶函数在对称区间的单调性相反.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
若动圆与圆(x+2)2+y2=4外切且与直线x=2相切,则动圆圆心的轨迹方程是( )
| A、y2-12x+12=0 |
| B、y2+12x-12=0 |
| C、y2+8x=0 |
| D、y2-8x=0 |

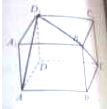 如图,已知ABCD-A1B1C1D1为正方体.
如图,已知ABCD-A1B1C1D1为正方体.