题目内容
设cos(
+α)=
,α∈(π,
),则tan2α的值是 .
| π |
| 2 |
| 1 |
| 2 |
| 3π |
| 2 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:由条件利用诱导公式求得sinα=-
,可得α的值,从而求得2α 的值,从而求得tan2α 的值.
| 1 |
| 2 |
解答:
解:∵cos(
+α)=-sinα=
,α∈(π,
),
∴sinα=-
,α=
,2α=
,
∴tan2α=tan
=tan
=
,
故答案为:
.
| π |
| 2 |
| 1 |
| 2 |
| 3π |
| 2 |
∴sinα=-
| 1 |
| 2 |
| 7π |
| 6 |
| 7π |
| 3 |
∴tan2α=tan
| 7π |
| 3 |
| π |
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题主要考查诱导公式的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
双曲线
-
=1的渐近线方程为( )
| x2 |
| 9 |
| y2 |
| 25 |
A、y=
| ||
B、y=±
| ||
C、y=±
| ||
D、y=
|
椭圆
+y2=1的焦距比短轴长( )
| x2 |
| 10 |
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |

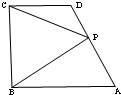 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设