题目内容
已知数列{an}满足a1=0,an+1-an=(1-an+1)(1-an).
(1)令cn=
,证明:数列{cn}是等差数列,并求出{an}的通项公式.
(2)设bn=
,其前n项和为Sn,证明:Sn<1.
(1)令cn=
| 1 |
| 1-an |
(2)设bn=
1-
| ||
|
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件得cn+1-cn=
-
=
=1,又c1=
=1,由此能证明数列{cn}是首项为1,公差为1的等差数列,并能求出an=1-
.
(2)bn=
=
=
-
,由此利用裂项求和法能证明Sn<1.
| 1 |
| 1-an+1 |
| 1 |
| 1-an |
| 1-an-(1-an+1) |
| (1-an+1)(1-an) |
| 1 |
| 1-a1 |
| 1 |
| n |
(2)bn=
1-
| ||
|
1-
| ||||
|
| 1 | ||
|
| 1 | ||
|
解答:
(1)证明:∵数列{an}满足a1=0,an+1-an=(1-an+1)(1-an),
cn=
,
∴cn+1-cn=
-
=
=
=1,
又c1=
=1,
∴数列{cn}是首项为1,公差为1的等差数列.
∴cn=
=1+n-1=n,
∴1-an=
,∴an=1-
.
(2)证明:∵bn=
=
=
=
-
,
∴Sn=(1-
)+(
-
)+…+(
-
)
=1-
<1,
∴Sn<1.
cn=
| 1 |
| 1-an |
∴cn+1-cn=
| 1 |
| 1-an+1 |
| 1 |
| 1-an |
=
| 1-an-(1-an+1) |
| (1-an+1)(1-an) |
=
| an+1-an |
| an+1-an |
又c1=
| 1 |
| 1-a1 |
∴数列{cn}是首项为1,公差为1的等差数列.
∴cn=
| 1 |
| 1-an |
∴1-an=
| 1 |
| n |
| 1 |
| n |
(2)证明:∵bn=
1-
| ||
|
1-
| ||||
|
1-
| ||||
|
| 1 | ||
|
| 1 | ||
|
∴Sn=(1-
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
=1-
| 1 | ||
|
∴Sn<1.
点评:本题考查等差数列的证明,考查数列的通项公式的求法,考查不等式的证明,解题时要注意裂项求和法的合理运用.

练习册系列答案
相关题目
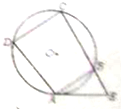 如图,四边形ABCD内接于圆O,点E在CB的延长线上,AE切圆于O于点A,若AB∥CD,AD=4
如图,四边形ABCD内接于圆O,点E在CB的延长线上,AE切圆于O于点A,若AB∥CD,AD=4| 3 |
| 3 |
| A、36 | ||
| B、6 | ||
| C、24 | ||
D、2
|
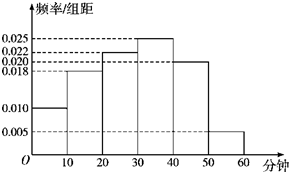 我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.如图是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图.将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?
我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.如图是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图.将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?