题目内容
设A,B是抛物线y2=4x上的点,且|AB|=8,则AB中点M的横坐标的最小值为( )
| A、4 | B、3 | C、2 | D、1 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用xM=
(xA+xB)=
(xA+
+xB+
)-
=
(|FA|+|FB|)-
,即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
解答:
解:由题意,xM=
(xA+xB)=
(xA+
+xB+
)-
=
(|FA|+|FB|)-
∵|FA|+|FB|≥|AB|=8,
∴xM≥4-1=3,
当A,F,B三点共线时,取得最小值.
故选:B.
| 1 |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
∵|FA|+|FB|≥|AB|=8,
∴xM≥4-1=3,
当A,F,B三点共线时,取得最小值.
故选:B.
点评:本题考查抛物线的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
相关题目
设p:
≤1,q:(x-a)•[x-(a+1)]≤0,若q是p的必要而不充分条件,则实数a的取值范围是( )
| 2x-1 |
A、[0,
| ||
B、(0,
| ||
C、(-∞,0)∪(
| ||
D、(-∞,0]∪[
|
设F1、F2分别是双曲线
-
=1(a>0,b>0)的左、右焦点,如双曲线上存在点P,使得∠PF1F2=30°,∠PF2F1=120°,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
直线a∥平面α,则a平行于平面α内的( )
| A、一条确定的直线 |
| B、任意一条直线 |
| C、所有的直线 |
| D、无穷多条平行直线 |
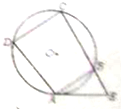 如图,四边形ABCD内接于圆O,点E在CB的延长线上,AE切圆于O于点A,若AB∥CD,AD=4
如图,四边形ABCD内接于圆O,点E在CB的延长线上,AE切圆于O于点A,若AB∥CD,AD=4| 3 |
| 3 |
| A、36 | ||
| B、6 | ||
| C、24 | ||
D、2
|
化简sin70°sin50°+cos110°cos50°的结果为( )
| A、cos20° | ||||
B、
| ||||
C、-
| ||||
D、
|