题目内容
设函数f(x)=|x-1|+|2x-a|,a∈R.
(Ⅰ)当a=4时,求不等式f(x)≥5的解集;
(Ⅱ)若f(x)≥4对x∈R恒成立,求a的取值范围.
(Ⅰ)当a=4时,求不等式f(x)≥5的解集;
(Ⅱ)若f(x)≥4对x∈R恒成立,求a的取值范围.
考点:绝对值不等式的解法
专题:不等式
分析:对第(1)问,将a的值代入f(x)中,令|x-1|=0,|2x-4|=0,将数轴分三段讨论即可得解集;
对第(2)问,根据函数f(x)=|x-1|+|2x-a|的图象特征,左边一段递减,右边一段递增,中间一段单调,且图象连续,图象的最低点必在转折处,由此知,函数f(x)的最小值为f(1)或f(
),只需f(x)min≥4即可.
对第(2)问,根据函数f(x)=|x-1|+|2x-a|的图象特征,左边一段递减,右边一段递增,中间一段单调,且图象连续,图象的最低点必在转折处,由此知,函数f(x)的最小值为f(1)或f(
| a |
| 2 |
解答:
解:(Ⅰ)a=4时,f(x)=|x-1|+|2x-4|,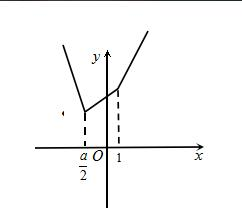
令|x-1|=0,得x=1;令|2x-4|=0,得x=2.
①当x≤1时,由f(x)=-(x-1)-(2x-4)=-3x+5≥5得x≤0,
∴x≤0.
②当1<x<2时,由f(x)=(x-1)-(2x-4)=-x+3≥5,得x≤-2,
∴原不等式无实数解.
③当x≥2时,由f(x)=(x-1)+(2x-4)=3x-5≥5,得x≥
,
∴x≥
.
综合①、②、③知,不等式f(x)≥5的解集为{x|x≤0,或x≥
}.
(Ⅱ)x=1时,f(x)=|2-a|;x=
时,f(x)=|
-1|.作出f(x)的图象,如右图所示,
要使f(x)≥4对x∈R恒成立,则
,得
得a≥10或a≤-6,故a的取值范围是[10,+∞)∪(-∞,-6].

令|x-1|=0,得x=1;令|2x-4|=0,得x=2.
①当x≤1时,由f(x)=-(x-1)-(2x-4)=-3x+5≥5得x≤0,
∴x≤0.
②当1<x<2时,由f(x)=(x-1)-(2x-4)=-x+3≥5,得x≤-2,
∴原不等式无实数解.
③当x≥2时,由f(x)=(x-1)+(2x-4)=3x-5≥5,得x≥
| 10 |
| 3 |
∴x≥
| 10 |
| 3 |
综合①、②、③知,不等式f(x)≥5的解集为{x|x≤0,或x≥
| 10 |
| 3 |
(Ⅱ)x=1时,f(x)=|2-a|;x=
| a |
| 2 |
| a |
| 2 |
要使f(x)≥4对x∈R恒成立,则
|
|
得a≥10或a≤-6,故a的取值范围是[10,+∞)∪(-∞,-6].
点评:本题考查了含两个绝对值符号的不等式的解法,及含参数的绝对值不等式恒成立问题,常规方法是利用零点分段法及函数的图象求解,体现了分类讨论的思想,数型结合思想等.其关键是找到“零点”或图象的“转折点”.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目

