题目内容

求函数y=
(x+1)2+1
+
(x-3)2+4
的值域．
考点：函数的值域
专题：计算题,函数的性质及应用
分析：利用数形结合法求函数的值域．
解答： 解：函数y=
(x+1)2+1
+
(x-3)2+4
的几何意义是点（x，0）到点（-1，1），（3，-2）的距离之和，
故
(x+1)2+1
+
(x-3)2+4
≥
(-1-3)2+(1+2)2
=5；
故函数y=
(x+1)2+1
+
(x-3)2+4
的值域为[5，+∞）．
点评：本题考查了函数值域的求法．高中函数值域求法有：1、观察法，2、配方法，3、反函数法，4、判别式法；5、换元法，6、数形结合法，7、不等式法，8、分离常数法，9、单调性法，10、利用导数求函数的值域，11、最值法，12、构造法，13、比例法．要根据题意选择．
练习册系列答案
相关题目
已知a＞0，函数f（x）=x|x-a|+1（x∈R）．
（Ⅰ）当a=1时，求所有使f（x）=x成立的x的值；
（Ⅱ）当a=1时，求函数y=f（x）在闭区间[0，2]上的最大值和最小值；
（Ⅲ）试讨论函数y=f（x）的图象与直线y=a的交点个数．
已知向量
a
、
b
满足|
a
|=1，|
b
|=4，且
a
•
b
=2，则
a
与
b
的夹角为（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
2
求函数y=
x
+3
3x2
+6
6x5
+a5（a为常数）的导数．
解不等式：|x-1|+|x-3|＞4．
设数列1，1+
1
2
，1+
1
2
+
1
22
，…，1+
1
2
+
1
22
+…+
1
2n-1
，…的前n项和为Sn，则
lim
n→∞
（Sn-2n）的值为（　　）
A、2B、0C、1D、-2
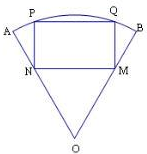如图，在半径为1，圆心角为60°的扇形AB弧上任取一点P，作扇形的内接矩形PNMQ，使点N、M分别在半径OA、OB上，点Q在
AB
上，求这个矩形面积的最大值．
已知幂函数f（x）=xm-3，m是正整数的图象关于y轴对称，且在区间（0，+∞）是减函数，求f（x）的解析式．
已知函数f（x）是定义在R上的偶函数，且f（x+1）为奇函数．若f（2）=1，则f（1）+f（2）+f（3）+…+f（2014）=（　　）
A、1B、2014
C、0D、-2014

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网