Question

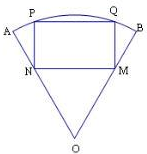如图，在半径为1，圆心角为60°的扇形AB弧上任取一点P，作扇形的内接矩形PNMQ，使点N、M分别在半径OA、OB上，点Q在

AB

上，求这个矩形面积的最大值．

Answer 1

考点：扇形面积公式

专题：三角函数的求值

分析：如图所示，取

AB

的中点E，连接OE分别交PQ、MN于F、G点，连接OP．设∠POE=θ.(θ∈(0，

π

6

))．可得PF=sinθ，OF=cosθ．又OG=

NG

tan30°

=

3

sinθ．可得FG=OF-OG=cosθ-

3

sinθ．因此这个矩形面积S=2sinθ(cosθ-

3

sinθ)=2sin(2θ+

π

3

)-

3

，利用三角函数的单调性即可得出．

解答： 解：如图所示，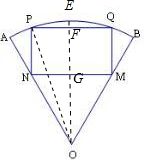
取

AB

的中点E，连接OE分别交PQ、MN于F、G点，连接OP．
设∠POE=θ.(θ∈(0，

π

6

))．
则PF=sinθ，OF=cosθ．
又OG=

NG

tan30°

=

3

sinθ．
∴FG=OF-OG=cosθ-

3

sinθ．
∴这个矩形面积S=2sinθ(cosθ-

3

sinθ)
=sin2θ-

3

(1-cos2θ)
=2sin(2θ+

π

3

)-

3

∵θ∈(0，

π

6

)，∴(2θ+

π

3

)∈(

π

3

，

2π

3

)．
∴当2θ+

π

3

=

π

2

，即θ=

π

12

时，sin(2θ+

π

3

)取得最大值1．
∴这个矩形面积的最大值是2-

3

．

点评：本题考查了三角函数的单调性、倍角公式、两角和差的正弦公式、矩形的面积计算公式、直角三角形的边角关系，考查了推理能力与计算能力，属于难题．