题目内容
已知平面α和β是空间中两个不同的平面，下列叙述中，正确的是 ．（填序号）
①因为M∈α，N∈α，所以MN∈α；
②因为M∈α，N∈β，所以α∩β=MN；
③因为AB?α，M∈AB，N∈AB，所以MN∈α；
④因为AB?α，AB?β，所以α∩β=AB．
①因为M∈α，N∈α，所以MN∈α；
②因为M∈α，N∈β，所以α∩β=MN；
③因为AB?α，M∈AB，N∈AB，所以MN∈α；
④因为AB?α，AB?β，所以α∩β=AB．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：当直线a在平面α内时，应表示为：a?α，而不是a∈α，可判断①③；根据面面相交的几何特征，可判断②④．
解答：
解：①若M∈α，N∈α，则MN?α，故错误；
②若M∈α，N∈β，则α与β可能平行也可能相交，即使相交交线也不一定为MN，故错误；
③若AB?α，M∈AB，N∈AB，则MN?α，故错误；
④若AB?α，AB?β，中α∩β=AB，故正确．
故正确的命题为：④，
故答案为：④
②若M∈α，N∈β，则α与β可能平行也可能相交，即使相交交线也不一定为MN，故错误；
③若AB?α，M∈AB，N∈AB，则MN?α，故错误；
④若AB?α，AB?β，中α∩β=AB，故正确．
故正确的命题为：④，
故答案为：④
点评：本题考查的知识点是平面的基本性质，空间点线面之间关系的符号表示，难度不大，属于基础题．
练习册系列答案
相关题目
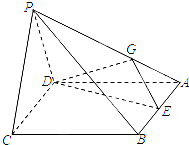如图，四棱锥P-ABCD中，底面ABCD为菱形，∠DAB=60°，平面PCD⊥底面ABCD，E是AB的中点，G为PA上的一点．