题目内容
4.已知数列{an}的前n项和为Sn,Sn=$\frac{1}{3}$(an-1)(n∈N*).(1)求a1,a2,a3的值;
(2)求an的通项公式及S10.
分析 (1)利用递推关系即可得出;
(2)利用等比数列的通项公式及其前n项和公式即可得出.
解答 解:(1)∵Sn=$\frac{1}{3}$(an-1)(n∈N*).
∴${a}_{1}=\frac{1}{3}({a}_{1}-1)$,a1+a2=$\frac{1}{3}({a}_{2}-1)$,a1+a2+a3=$\frac{1}{3}$(a3-1),
联立解得a1=-$\frac{1}{2}$,a2=$\frac{1}{4}$,a3=$-\frac{1}{8}$.
(2)由Sn=$\frac{1}{3}$(an-1),当n≥2时,an=Sn-Sn-1=$\frac{1}{3}$(an-1)-$\frac{1}{3}$(an-1-1),
化为:${a}_{n}=-\frac{1}{2}{a}_{n-1}$.
∴数列{an}是等比数列,首项与公比都为-$\frac{1}{2}$.
∴an=$(-\frac{1}{2})^{n}$.
Sn=$\frac{-\frac{1}{2}[1-(-\frac{1}{2})^{n}]}{1-(-\frac{1}{2})}$=-$\frac{1}{3}$$[1-(-\frac{1}{2})^{n}]$.
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.已知集合A={x|log2x<2},B={y|y=3x+2,x∈R},则A∩B=( )
| A. | (1,4) | B. | (2,4) | C. | (1,2) | D. | (1,+∞) |
19.命题p:?x∈N,x3<x2;命题q:?a∈(0,1)∪(1,+∞),函数f(x)=loga(x-1)的图象过点(2,0),则下列命题是真命题的是( )
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
9.已知函数$f(x)=asinx-\sqrt{3}cosx$关于直线$x=-\frac{π}{6}$对称,且f(x1)•f(x2)=-4,则|x1+x2|的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
13.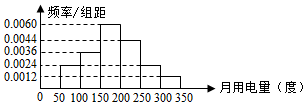 为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )
为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )
 为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )
为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )| A. | 70 | B. | 64 | C. | 48 | D. | 30 |
4.已知i为虚数单位,若复数i•z=$\sqrt{2}$-i,则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\frac{{\sqrt{6}}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\frac{{\sqrt{6}}}{2}$.