题目内容
数列{an}中,a1=a2=1,an+2=an+1+an,它的通项公式为an=
[(
)n-(
)n],根据上述结论,可以知道不超过实数
(
)12的最大整数为( )
| 1 | ||
|
1+
| ||
| 2 |
1-
| ||
| 2 |
| 1 | ||
|
1+
| ||
| 2 |
| A、144 |
| B、143 |
| C、144或143 |
| D、142或143 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:先根据递推关系求出a12,然后根据0<(
)12<1,可得到实数
(
)12的范围,从而求出不超过实数
(
)12的最大整数.
1-
| ||
| 2 |
| 1 | ||
|
1+
| ||
| 2 |
| 1 | ||
|
1+
| ||
| 2 |
解答:
解:∵a1=a2=1,an+2=an+1+an,
∴a3=2,依此类推得a4=3,a5=5,a6=8,a7=13,a8=21,
a9=34,a10=55,a11=89,a12=144,
∵0<(
)12<1,
∴a12=144=
[(
)12-(
)12]<
(
)12.
∴不超过实数
(
)12的最大整数为144.
故选:A.
∴a3=2,依此类推得a4=3,a5=5,a6=8,a7=13,a8=21,
a9=34,a10=55,a11=89,a12=144,
∵0<(
1-
| ||
| 2 |
∴a12=144=
| 1 | ||
|
1+
| ||
| 2 |
1-
| ||
| 2 |
| 1 | ||
|
1+
| ||
| 2 |
∴不超过实数
| 1 | ||
|
1+
| ||
| 2 |
故选:A.
点评:本题主要考查了数列的应用,解答的关键是由数列递推式求出a12=144,考查了放缩法证明数列不等式,属于有一定难度题目.

练习册系列答案
相关题目
已知集合A={x|x2-2x<0},B={y|y=2x,x>0},R是实数集,则(∁RB)∩A等于( )
| A、[0,1] |
| B、(0,1] |
| C、(-∞,0] |
| D、[1,+∞] |
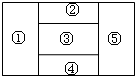 如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有( )种.
如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有( )种.| A、36 | B、24 | C、72 | D、48 |