题目内容
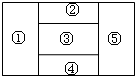如图所示，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着方法共有（ ）种．| A、36 | B、24 | C、72 | D、48 |
考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：根据题意，分2种情况讨论：若选3种颜色时，就是②④同色，①⑤同色；若4种颜色全用，只能②④或①⑤用一种颜色，其它不相同，求解即可．
解答：
解：由题意，选用3种颜色时，必须是②④同色，①⑤同色，与③进行全排列，
涂色方法有C43•A33=24种
4色全用时涂色方法：是②④同色或①⑤同色，有2种情况，
涂色方法有C21•A44=48种
所以不同的着色方法共有48+24=72种；
故选：C．．
涂色方法有C43•A33=24种
4色全用时涂色方法：是②④同色或①⑤同色，有2种情况，
涂色方法有C21•A44=48种
所以不同的着色方法共有48+24=72种；
故选：C．．
点评：本题考查计数原理的应用，涉及分类讨论，解题时注意结合题意中的图形分析．
练习册系列答案
相关题目
数列{an}中，a1=a2=1，an+2=an+1+an，它的通项公式为an=
[（
）n-（
）n]，根据上述结论，可以知道不超过实数
（
）12的最大整数为（ ）
| 1 | ||
|
1+
| ||
| 2 |
1-
| ||
| 2 |
| 1 | ||
|
1+
| ||
| 2 |
| A、144 |
| B、143 |
| C、144或143 |
| D、142或143 |
如图，线段AB夹在一个直二面角的两个半平面内，它与两个半平面所成角都是30°，则AB与这个二面角的棱l所成角为（ ）| A、30° | B、45° |
| C、60° | D、90° |
设数列{an} 的前n项和为 Sn，令Tn=
，称 Tn为数列 a1，a2，…，an的“理想数“，已知数列a1，a2，…，a20的“理想数“为21，那么数列2，a1，a2，…，a20 的“理想数”为（ ）
| S1+S2+…+Sn |
| n |
| A、23 | B、24 | C、22 | D、20 |
已知不等式|x-m|＜1成立的一个充分非必要条件是
＜x＜
，则实数m的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、(-∞，-
| ||||
D、[
|
平面内△ABC及一点O满足
•
=
•
，
•
=
•
，则点O是△ABC的（ ）
| AO |
| AB |
| BO |
| BA |
| BO |
| BC |
| CO |
| CB |
| A、重心 | B、垂心 | C、内心 | D、外心 |