题目内容
函数y=|3x-x3|在区间[-2,2]上的最大值为 .
考点:利用导数求闭区间上函数的最值
专题:计算题,导数的概念及应用
分析:令f(x)=3x-x3,确定函数的单调性,求出函数在区间[-2,2]上的最值,即可得出结论.
解答:
解:令f(x)=3x-x3,则f′(x)=3-3x2,
由f′(x)=0,可得x=±1,
∴函数f(x)=3x-x3在区间[-2,2]上的递增区间为[-1,1],递减区间为[-2,-1],[1,2],
∵f(-2)=2,f(-1)=-2,f(1)=2,f(2)=-2,
∴函数y=|3x-x3|在区间[-2,2]上的最大值为2
故答案为:2.
由f′(x)=0,可得x=±1,
∴函数f(x)=3x-x3在区间[-2,2]上的递增区间为[-1,1],递减区间为[-2,-1],[1,2],
∵f(-2)=2,f(-1)=-2,f(1)=2,f(2)=-2,
∴函数y=|3x-x3|在区间[-2,2]上的最大值为2
故答案为:2.
点评:本题考查利用导数求闭区间上函数的最值,考查函数的单调性,考查学生的计算能力,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
数列{an}中,a1=a2=1,an+2=an+1+an,它的通项公式为an=
[(
)n-(
)n],根据上述结论,可以知道不超过实数
(
)12的最大整数为( )
| 1 | ||
|
1+
| ||
| 2 |
1-
| ||
| 2 |
| 1 | ||
|
1+
| ||
| 2 |
| A、144 |
| B、143 |
| C、144或143 |
| D、142或143 |
已知抛物线y2=ax(a>0),直线l过焦点F且与x轴不重合,则抛物线被l垂直平分的弦( )
| A、不存在 | B、有且仅有一条 |
| C、有2条 | D、有3条 |
 如图,线段AB夹在一个直二面角的两个半平面内,它与两个半平面所成角都是30°,则AB与这个二面角的棱l所成角为( )
如图,线段AB夹在一个直二面角的两个半平面内,它与两个半平面所成角都是30°,则AB与这个二面角的棱l所成角为( )| A、30° | B、45° |
| C、60° | D、90° |
已知不等式|x-m|<1成立的一个充分非必要条件是
<x<
,则实数m的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、[
|
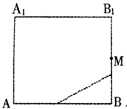
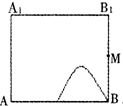
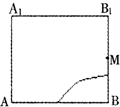
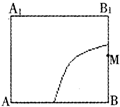
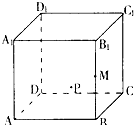 如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到平面A1C1的距离是直线BC的距离的2倍,点M是棱BB1的中点,则动点P所在曲线的大致形状为( )
如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到平面A1C1的距离是直线BC的距离的2倍,点M是棱BB1的中点,则动点P所在曲线的大致形状为( )