题目内容
能表示定义域为M={x|0≤x≤2},值域为N={y|1≤y≤2}的函数是( )
A、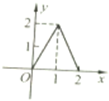 |
B、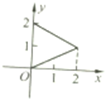 |
C、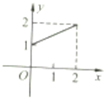 |
D、 |
考点:函数的概念及其构成要素
专题:函数的性质及应用
分析:根据函数的概念,结合函数的定义域,值域判断即可.
解答:
解:∵义域为M={x|0≤x≤2},值域为N={y|1≤y≤2}的函数,
∴根据函数的概念可得出:C图象符合,A值域不符合,B的图象1个x 值有2个y值对应了,故B不符合,D的定义域不符合,
故选:C
∴根据函数的概念可得出:C图象符合,A值域不符合,B的图象1个x 值有2个y值对应了,故B不符合,D的定义域不符合,
故选:C
点评:本题考查了函数的概念,运用图象判断定义域,值域,属于容易题.

练习册系列答案
相关题目
数列{an}中,a1=a2=1,an+2=an+1+an,它的通项公式为an=
[(
)n-(
)n],根据上述结论,可以知道不超过实数
(
)12的最大整数为( )
| 1 | ||
|
1+
| ||
| 2 |
1-
| ||
| 2 |
| 1 | ||
|
1+
| ||
| 2 |
| A、144 |
| B、143 |
| C、144或143 |
| D、142或143 |