题目内容
6.函数f(x)=sin(ωx)(ω>0)在区间$[0,\frac{π}{4}]$上单调递增,在区间$[\frac{π}{4},\frac{π}{3}]$上单调递减,则ω为( )| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
分析 由单调区间可知f($\frac{π}{4}$)=1.
解答 解:∵f(x)在区间$[0,\frac{π}{4}]$上单调递增,在区间$[\frac{π}{4},\frac{π}{3}]$上单调递减,
∴fmax(x)=f($\frac{π}{4}$)=1,且($\frac{π}{4}$,1)为f(x)在第一象限内的第一个最高点,
∴sin$\frac{ωπ}{4}$=1,$\frac{ωπ}{4}$=$\frac{π}{2}$,∴ω=2.
故选B.
点评 本题考查了正弦函数的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.若关于x的方程ax-x-a=0有两个不同的实数根,则实数a的取值范围为( )
| A. | (0,+∞) | B. | (0,1) | C. | (0,2) | D. | (1,+∞) |
1.利用独立性检验的方法调查大学生的性别与爱好某项运动是否有关,通过随机询问110名不同的大学生是否爱好某项运动,利用2×2列联表,由计算可得K2≈8.806
参照附表,得到的正确结论是( )
| P(K2>k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%以上的把握认为“爱好该项运动与性别无关” | |
| B. | 有99.5%以上的把握认为“爱好该项运动与性别有关” | |
| C. | 在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别无关” |
18.若$cos(π+α)=-\frac{{\sqrt{3}}}{2}$,$\frac{3}{2}π<α<2π$,则sin(2π-α)=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $±\frac{1}{2}$ |
15.已知等差数列{an}的前$n项和为{S_n},若\overrightarrow{OC}={a_1}\overrightarrow{OA}+{a_{2015}}\overrightarrow{OB}$,且满足条件$\overrightarrow{AC}=2\overrightarrow{CB},则{S_{2015}}$=( )
| A. | $\frac{2016}{2}$ | B. | 2016 | C. | $\frac{2015}{2}$ | D. | 2015 |
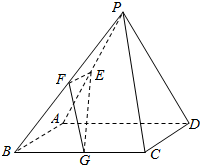 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,且平面PAD⊥平面ABCD,E,F,G分别是PA、PB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,且平面PAD⊥平面ABCD,E,F,G分别是PA、PB、BC的中点.