题目内容
14.某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题: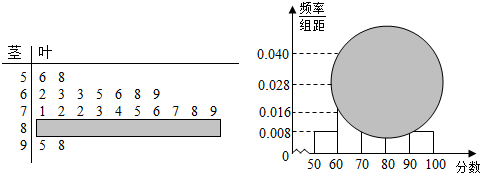
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)若规定:90分(包含90分)以上为优秀,现从分数在80分(包含80分)以上的试卷中任取两份分析学生失分情况,求在抽取的试卷中至少有一份优秀的概率.
分析 (I)分数在[50,60)的频率为第一组矩形的面积,全班人数为该组的频数与频率的比值;
(II)用全班人数减去其余组的人数即为[80,90)之间的频数,用该组的频率与组距的比值为矩形的高;
(III)对符合条件的试卷进行编号,使用列举法求出基本事件个数和符合条件的基本事件个数,得出概率.
解答 解:(1)分数在[50,60)的频率为0.008×10=0.08
由茎叶图知:分数在[50,60)之间的频数为2,所以全班人数为$\frac{2}{0.08}$=25
(2)分数在[80,90)之间的频数为25-2-7-10-2=4
频率分布直方图中[80,90)间的矩形的高为$\frac{4}{25}$÷10=0.016
(3)由(2)可知分数分数在[80,100)的人数为4+2=6,设分数在[80,90)的试卷为A,B,C,D,分数在[90,100)的试卷为a,b.
则从6分试卷中任取两份共有15个基本事件,分别是AB,AC,AD,Aa,Ab,BC,BD,Ba,Bb,CD,Ca,Cb,Da,Db,ab.
其中至少有一份优秀共有9个基本事件,分别是Aa,Ab,Ba,Bb,Ca,Cb,Da,Db,ab,
∴抽取的试卷中至少有一份优秀的概率P=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查了茎叶图与频率分布直方图,古典概型的概率计算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.P是△ABC内一点,△ACP,△BCP的面积分别记为S1,S2,已知$\overrightarrow{CP}=\frac{2λ}{3}\overrightarrow{CA}+\frac{λ}{3}\overrightarrow{CB}$,其中λ∈(0,1),则$\frac{S_1}{S_2}$=( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
6.函数f(x)=sin(ωx)(ω>0)在区间$[0,\frac{π}{4}]$上单调递增,在区间$[\frac{π}{4},\frac{π}{3}]$上单调递减,则ω为( )
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
4.下列函数中,是偶函数的是( )
| A. | y=2x | B. | y=x2 | C. | y=2x | D. | y=log2x |