题目内容
12.已知函数f(x)=|x+1|+|2x-4|.(Ⅰ)解关于x的不等式f(x)<9;
(Ⅱ)若直线y=m与函数y=f(x)的图象围成一个三角形,求实数m的取值范围,并求围成的三角形面积的最大值.
分析 (Ⅰ)分类讨论以去掉绝对值号,即可解关于x的不等式f(x)<9;
(Ⅱ)作出函数的图象,结合图象求解.
解答 解:(Ⅰ)x≤-1,不等式可化为-x-1-2x+4<9,
x>-2,∴-2<x≤-1;
-1<x<2,不等式可化为x+1-2x+4<9,∴x>-4,∴-1<x<2;
x≥2,不等式可化为x+1+2x-4<9,∴x<4,∴2≤x<4;
综上所述,不等式的解集为{x|-2<x<4};
(Ⅱ)f(x)=|x+1|+2|x-2|,
由题意作图如下,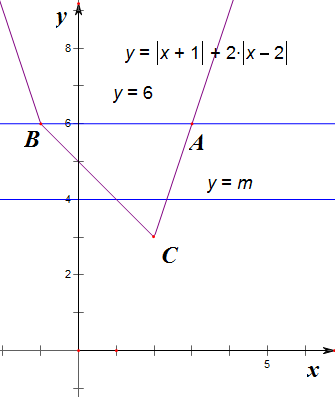 ,
,
结合图象可知,A(3,6),B(-1,6),C(2,3);
故3<m≤6,
且m=6时面积最大为$\frac{1}{2}$×(3+1)×3=6.
点评 本题考查了绝对值函数的应用及数形结合的思想方法应用,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
2.甲、乙两人约定晚6点到晚7点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率( )
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
20.设集合A={0,1,2},B={x|(x+1)(x-2)<0},则A∩B的元素个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
7.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x,x≥0}\\{-3x,x<0}\end{array}\right.$,若a[f(a)-f(-a)]>0,则实数a的取值范围为( )
| A. | (1,+∞) | B. | (2,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-2)∪(2,+∞) |
4.随着人口老龄化的到来,我国的劳动力人口在不断减少,”延迟退休“已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
经调查年龄在[25,30),[55,60)的被调查者中赞成人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为X,求随机变量X的分布列和数学期望.
| 年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 人数 | 4 | 5 | 8 | 5 | 3 |
| 年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
| 人数 | 6 | 7 | 3 | 5 | 4 |
(Ⅰ)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为X,求随机变量X的分布列和数学期望.
1.若集合A={x|(x+4)(x+1)<0},集合B={x|x<-2},则A∩(∁RB)等于( )
| A. | (-2,-1) | B. | [-2,4) | C. | [-2,-1) | D. | ∅ |