题目内容
已知P点在y轴上,点Q在x轴的正半轴上,点H(-3,0),E(-1,0),点M在直线PQ上,且满足
•
=0,
=-
.当点P在y轴上移动时,记点M的轨迹为G.在轨迹G上经过点F(1,0)作弦AB
(1)求轨迹G的方程;
(2)若
=λ
,求证:
⊥(
-λ
).
| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
(1)求轨迹G的方程;
(2)若
| AF |
| FB |
| EF |
| EA |
| EB |
考点:平面向量数量积的运算,轨迹方程
专题:计算题,证明题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:(1)设出M的坐标,利用题意向量的关系,求得x和y的关系,进而求得M的轨迹G的方程;
(2)设A(x1,y1),B(x2,y2),直线AB:y=k(x-1),运用抛物线的定义和联立直线方程和抛物线方程,运用韦达定理,求出x1=λ,x2=
,求得|AE|=λ|EB|,再由向量垂直的条件,即可得证.
(2)设A(x1,y1),B(x2,y2),直线AB:y=k(x-1),运用抛物线的定义和联立直线方程和抛物线方程,运用韦达定理,求出x1=λ,x2=
| 1 |
| λ |
解答:
(1)解:设点M的坐标为(x,y),
由
=-
,得P(0,-
),Q(
,0),
由
•
=0,得(3,-
)•(x,
y)=0,
所以y2=4x,由点Q在x轴的正半轴上,得x>0,
即轨迹方程为y2=4x(x>0);
(2)证明:动点M的轨迹C是以(0,0)为顶点,
以(1,0)为焦点的抛物线,除去原点.
设A(x1,y1),B(x2,y2),
直线AB:y=k(x-1),代入抛物线方程,可得,
k2x2-(2k2+4)x+k2=0,则x1x2=1,
由抛物线的定义可得|AF|=x1+1,|BF|=x2+1,
由于
=λ
,则有x1+1=λ(x2+1),
解得,x1=λ,x2=
,
则有|AE|=
=
,
|BE|=
=
,
则有|AE|=λ|EB|,
则有
•(
-λ
)=
•(
-λ
)
=
(
2-λ2
2)=0,
则有
⊥(
-λ
).
由
| PM |
| 3 |
| 2 |
| MQ |
| y |
| 2 |
| x |
| 3 |
由
| HP |
| PM |
| y |
| 2 |
| 3 |
| 2 |
所以y2=4x,由点Q在x轴的正半轴上,得x>0,
即轨迹方程为y2=4x(x>0);
(2)证明:动点M的轨迹C是以(0,0)为顶点,
以(1,0)为焦点的抛物线,除去原点.
设A(x1,y1),B(x2,y2),
直线AB:y=k(x-1),代入抛物线方程,可得,
k2x2-(2k2+4)x+k2=0,则x1x2=1,
由抛物线的定义可得|AF|=x1+1,|BF|=x2+1,
由于
| AF |
| FB |
解得,x1=λ,x2=
| 1 |
| λ |
则有|AE|=
| (x1+1)2+y12 |
| x12+6x1+1 |
|BE|=
| (x2+1)2+y22 |
| x22+6x2+1 |
则有|AE|=λ|EB|,
则有
| EF |
| EA |
| EB |
| ||||
| 1+λ |
| EA |
| EB |
=
| 1 |
| 1+λ |
| EA |
| EB |
则有
| EF |
| EA |
| EB |
点评:本题考查平面向量的数量积的坐标表示和性质,考查向量共线的性质,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
已知A(2,1),B(3,5),把
按向量(3,2)平移后得到一个新向量
,那么下面各向量中能与
垂直的是( )
| AB |
| CD |
| CD |
| A、(-3,-2) | ||||
B、(
| ||||
| C、(-4,1) | ||||
| D、(0,-2) |
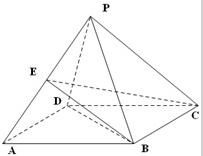 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=