题目内容
求函数y=sin|x|的单调区间.
考点:正弦函数的单调性
专题:三角函数的图像与性质
分析:画出函数y=sin|x|的图象,数形结合求得y=sin|x|的单调区间.
解答:
 解:函数y=sin|x|的图象如图所示:
解:函数y=sin|x|的图象如图所示:
故函数在(0,+∞)上的增区间为(0,
)、(2kπ-
,2kπ+
),k∈N+,
减区间为(2kπ+
,2kπ+
),k∈N+;
函数在(-∞,0)上的增区间为(-2kπ-
,-2kπ-
),k∈N+,
减区间为(-
,0)、(-2kπ-
,-2kπ+
),k∈N+.
 解:函数y=sin|x|的图象如图所示:
解:函数y=sin|x|的图象如图所示:故函数在(0,+∞)上的增区间为(0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
减区间为(2kπ+
| π |
| 2 |
| 3π |
| 2 |
函数在(-∞,0)上的增区间为(-2kπ-
| 3π |
| 2 |
| π |
| 2 |
减区间为(-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
点评:本题主要考查正弦函数的图象特征,正弦函数的单调性,体现了数形结合的数学思想,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
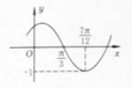 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
 如图,设O是?ABCD所在平面外的任一点,已知
如图,设O是?ABCD所在平面外的任一点,已知