题目内容
已知1≤x2+y2≤2,求证:
≤x2-xy+y2≤3.
| 1 |
| 2 |
考点:不等式的证明,三角函数的最值
专题:推理和证明
分析:设x=rcosθ,y=rsinθ,其中1≤r2≤2,0≤θ<2π,化简x2-xy+y2=r2-r2sin2θ=r2(1-
sin2θ),通过三角函数的有界性证明
≤x2-xy+y2≤3.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
(文)证明:∵1≤x2+y2≤2,∴可设x=rcosθ,y=rsinθ,其中1≤r2≤2,0≤θ<2π
∴x2-xy+y2=r2-r2sin2θ=r2(1-
sin2θ),
∵
≤1-
sin2θ≤
,∴
r2≤r2(1-
sin2θ)≤
r2,
而
r2≥
,
r2≤3∴
≤x2-xy+y2≤3.
∴x2-xy+y2=r2-r2sin2θ=r2(1-
| 1 |
| 2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
而
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查不等式的证明,三角函数的有界性的应用,三角函数的最值,考查计算与推理能力.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
某空间几何体的三视图如图所示,则该几何体的体积为( )


| A、180 | ||
| B、240 | ||
C、12
| ||
| D、264 |
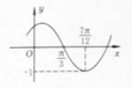 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
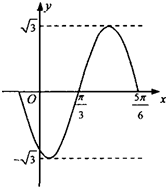 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|