题目内容
已知实数x,y满足约束条件
,则z=5-x2-y2的最大值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,结合数形结合即可得到结论.
解答:
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由z=5-x2-y2,得x2+y2=5-z,
则5-z的几何意义为区域内的动点P到原点距离的平方,
则由图象可知当点位于点O在直线x+y=3上的垂足A时,
此时|OA|的距离最小,对应的z最大,
则|OA|=
=
,
∴5-z=|OA|2=
,
∴zmax=5-
=
,
故答案为:
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:由z=5-x2-y2,得x2+y2=5-z,
则5-z的几何意义为区域内的动点P到原点距离的平方,
则由图象可知当点位于点O在直线x+y=3上的垂足A时,
此时|OA|的距离最小,对应的z最大,
则|OA|=
| |3| | ||
|
3
| ||
| 2 |
∴5-z=|OA|2=
| 9 |
| 2 |
∴zmax=5-
| 9 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查线性规划的应用,以及点到直线的距离公式,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
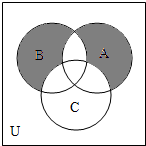 如图所示,已知集合A、B、C为全集U的子集,则图中阴影部分所表示的集合为( )
如图所示,已知集合A、B、C为全集U的子集,则图中阴影部分所表示的集合为( )| A、(∁∪C)∪(A∪B) |
| B、(A∪B)∩[∁∪(A∩B)] |
| C、(A∪B)∩[∁∪(A∩B∩C)] |
| D、{A∩[∁∪(B∪C)]}∪{B∩[∁∪(A∪C)]} |
 已知四棱锥P-ABCD的底面是等腰梯形,AD=BC=1,DC=2AB=2PD,∠ADC=60°,PD⊥底面ABCD,试建立空间直角坐标系,并表示五个点的坐标.
已知四棱锥P-ABCD的底面是等腰梯形,AD=BC=1,DC=2AB=2PD,∠ADC=60°,PD⊥底面ABCD,试建立空间直角坐标系,并表示五个点的坐标.