题目内容
设全集为实数集R,集合A={x|
≤x≤3},B={x||x|+a<0}.若(∁RA)∩B=B,求实数a的取值范围.
| 1 |
| 2 |
考点:交、并、补集的混合运算
专题:集合
分析:根据已知求出∁RA={x|x<
,或x>3},进而对a进行分类讨论,最后综合讨论结果可得实数a的取值范围.
| 1 |
| 2 |
解答:
解:∵集合A={x|
≤x≤3},
∴∁RA={x|x<
,或x>3},
若(∁RA)∩B=B,则B⊆∁RA,
若a≥0,则B=∅,满足条件,
若a<0,则B={x|a<x<-a},此时满足B⊆∁RA的a值不存在,
综上所述实数a的取值范围为a≥0
| 1 |
| 2 |
∴∁RA={x|x<
| 1 |
| 2 |
若(∁RA)∩B=B,则B⊆∁RA,
若a≥0,则B=∅,满足条件,
若a<0,则B={x|a<x<-a},此时满足B⊆∁RA的a值不存在,
综上所述实数a的取值范围为a≥0
点评:本题考查的知识点是子集,补集及其运算,难度不大,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图所示,在四面体P-ABC中,PC⊥平面ABC,AB=BC=CA=PC,那么二面角B-AP-C的余弦值为( )
如图所示,在四面体P-ABC中,PC⊥平面ABC,AB=BC=CA=PC,那么二面角B-AP-C的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
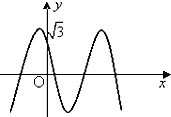 如图,函数f(x)=2cos(ωx+θ)(x∈R,ω>0,0≤θ≤
如图,函数f(x)=2cos(ωx+θ)(x∈R,ω>0,0≤θ≤