题目内容
正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别是DC、DD1、A1D1、A1B1、BB1、BC的中点,O为底面中心,求证:这六点共面.
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:接EF、FG、GH、HK、KL、LE、EG、LH、BD、B1D1,则EL∥BD,GH∥B1D1,BD∥B1D1,从而EL∥GH,过EL、GH做平面ELHG,E、L、H、G共面,设EG、LH与平面BDB1D1的交点分别为P、Q,则PQ∥EL∥GH,且P、Q分别为GE、LH的中点,由此能证明E、F、G、H、K、L这六点共面.
解答:
证明:接EF、FG、GH、HK、KL、LE、EG、LH、BD、B1D1,
E、L、G、H分别为CD、BC、A1D1、A1B1中点,
则EL∥BD,GH∥B1D1,BD∥B1D1,
则EL∥GH,过EL、GH做平面ELHG,
E、L、H、G共面,设EG、LH与平面BDB1D1的交点分别为P、Q,
则PQ∥EL∥GH,且P、Q分别为GE、LH的中点,
连接FP、KQ,则FP∥BD∥KQ,
F、P、Q、K共线,F、K在平面ELHG内,
所以E、F、G、H、K、L这六点共面.
E、L、G、H分别为CD、BC、A1D1、A1B1中点,
则EL∥BD,GH∥B1D1,BD∥B1D1,
则EL∥GH,过EL、GH做平面ELHG,
E、L、H、G共面,设EG、LH与平面BDB1D1的交点分别为P、Q,
则PQ∥EL∥GH,且P、Q分别为GE、LH的中点,
连接FP、KQ,则FP∥BD∥KQ,
F、P、Q、K共线,F、K在平面ELHG内,
所以E、F、G、H、K、L这六点共面.
点评:本题考查六点共面的证明,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
| A、0.852 |
| B、0.819 2 |
| C、0.8 |
| D、0.75 |
 如图所示,在四面体P-ABC中,PC⊥平面ABC,AB=BC=CA=PC,那么二面角B-AP-C的余弦值为( )
如图所示,在四面体P-ABC中,PC⊥平面ABC,AB=BC=CA=PC,那么二面角B-AP-C的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若lga,lgb是方程2x2-4x+1=0两个根,则(lg
)2值等于( )
| a |
| b |
| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
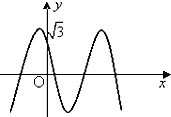 如图,函数f(x)=2cos(ωx+θ)(x∈R,ω>0,0≤θ≤
如图,函数f(x)=2cos(ωx+θ)(x∈R,ω>0,0≤θ≤