题目内容
在[-1,2]上随机取一个实数,则|x-1|≤1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:由条件知-1≤x≤2,然后解不等式的解,根据几何概型的概率公式即可得到结论.
解答:
解:在区间[-1,2]之间随机抽取一个数x,则-1≤x≤2,
由|x-1|≤1得-1≤x-1≤1,即得0≤x≤2,
∴根据几何概型的概率公式可知满足|x-1|≤1的概率为
=
,
故选:A
由|x-1|≤1得-1≤x-1≤1,即得0≤x≤2,
∴根据几何概型的概率公式可知满足|x-1|≤1的概率为
| 2-0 |
| 2-(-1) |
| 2 |
| 3 |
故选:A
点评:本题主要考查几何概型的概率的计算,根据不等式的性质解出不等式的是解决本题的关键,比较基础.

练习册系列答案
相关题目
若实数x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、-1 | B、2 | C、1 | D、0 |
已知集合A={x|x2-2x<0},B={x|x≤-1或x>1},则A∩(∁RB)=( )
| A、{x|0<x<1} |
| B、{x|1≤x<2} |
| C、{x|0<x≤1} |
| D、{x|1<x<2} |
若x,y满足约束条件
,则函数z=2x-y的最大值是( )
|
| A、-1 | B、0 | C、3 | D、6 |
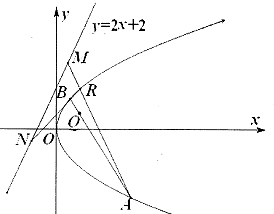 已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.
已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.