题目内容
17.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),O是坐标原点,F1,F2分别为其左右焦点,|F1F2|=2$\sqrt{3}$,M是椭圆上一点,∠F1MF2的最大值为$\frac{2}{3}$π(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C交于P,Q两点,且OP⊥OQ
(i)求证:$\frac{1}{{{{|{OP}|}^2}}}+\frac{1}{{{{|{OQ}|}^2}}}$为定值;
(ii)求△OPQ面积的取值范围.
分析 (Ⅰ)利用已知条件求出a=2,b=1,得椭圆方程.
(Ⅱ)i)当OP,OQ斜率都存在且不为0时,设lOP:y=kx,P(x1,y1),Q(x2,y2)联立直线与椭圆方程,求出PQ坐标,然后求解$\frac{1}{{{{|{OP}|}^2}}}+\frac{1}{{{{|{OQ}|}^2}}}$为定值.当OP,OQ斜率一个为0,一个不存在时,验证即可.ii) 当OP,OQ斜率都存在且不为0时,表示△OPQ面积,利用基本不等式求解面积的范围即可.
解答 解:(Ⅰ)由题意椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),O是坐标原点,F1,F2分别为其左右焦点,|F1F2|=2$\sqrt{3}$,M是椭圆上一点,∠F1MF2的最大值为$\frac{2}{3}$π,可得c=$\sqrt{3}$,2b=a,a2=b2+c2,
得a=2,b=1,得椭圆方程为:$\frac{x^2}{4}+{y^2}=1$…(4分)
(Ⅱ)i)当OP,OQ斜率都存在且不为0时,设lOP:y=kx,P(x1,y1),Q(x2,y2)
由$\left\{\begin{array}{l}y=kx\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$消y得${x_1}^2=\frac{4}{{1+4{k^2}}}$,${y_1}^2={k^2}{x_1}^2=\frac{{4{k^2}}}{{1+4{k^2}}}$
同理得${x_2}^2=\frac{{4{k^2}}}{{4+{k^2}}}$,${y_2}^2=\frac{1}{k^2}{x_2}^2=\frac{4}{{{k^2}+4}}$
故$\frac{1}{{{{|{OP}|}^2}}}+\frac{1}{{{{|{OQ}|}^2}}}=\frac{1}{{{x_1}^2+{y_1}^2}}+\frac{1}{{{x_2}^2+{y_2}^2}}=\frac{5}{4}$…(7分)
当OP,OQ斜率一个为0,一个不存在时,得$\frac{1}{{{{|{OP}|}^2}}}+\frac{1}{{{{|{OQ}|}^2}}}=\frac{1}{4}+\frac{1}{1}=\frac{5}{4}$
综上得$\frac{1}{{{{|{OP}|}^2}}}+\frac{1}{{{{|{OQ}|}^2}}}=\frac{5}{4}$,得证. …(8分)
(未讨论斜率这扣1分)
ii) 当OP,OQ斜率都存在且不为0时,${S_{OPQ}}=\frac{1}{2}\sqrt{O{P^2}•O{Q^2}}=\frac{1}{2}\sqrt{\frac{{4{k^2}+4}}{{1+4{k^2}}}•\frac{{4{k^2}+4}}{{{k^2}+4}}}$
=$2\sqrt{\frac{1}{{4+\frac{{9{k^2}}}{{{k^4}+2{k^2}+1}}}}}$
又$0<\frac{{9{k^2}}}{{{k^4}+2{k^2}+1}}≤\frac{{9{k^2}}}{{2\sqrt{{k^4}•1}+2{k^2}}}=\frac{9}{4}$
所以$\frac{4}{5}≤{S_{△OPQ}}<1$…..(11分)
当OP,OQ斜率一个为0,一个不存在时,S△OPQ=1
综上得$\frac{4}{5}≤{S_{△OPQ}}≤1$…(12分)
(未讨论斜率这扣1分)
点评 本题考查椭圆方程的求法,椭圆的简单性质的应用,直线与椭圆的位置关系的综合应用,考查分析问题解决问题的能力.

| A. | $4\sqrt{5}$ | B. | $8\sqrt{5}$ | C. | $4\sqrt{15}$ | D. | $8\sqrt{15}$ |
| A. | $({1,\sqrt{2}})$ | B. | $({1,\sqrt{3}})$ | C. | (1,2) | D. | (2,+∞) |
| A. | $[{kπ-\frac{π}{3},kπ+\frac{π}{6}}]$,(k∈Z) | B. | $[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}]$,(k∈Z) | ||
| C. | $[{kπ-\frac{7π}{12},kπ-\frac{π}{12}}]$,(k∈Z) | D. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}]$,(k∈Z) |
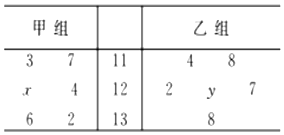 如图茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分),已知甲组数据的众数为124,乙组数据的平均数为甲组数据的中位数,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分),已知甲组数据的众数为124,乙组数据的平均数为甲组数据的中位数,则x,y的值分别为( )