题目内容
6．
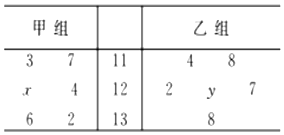如图茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩（单位：分），已知甲组数据的众数为124，乙组数据的平均数为甲组数据的中位数，则x，y的值分别为（ ）| A． | 4，4 | B． | 5，4 | C． | 4，5 | D． | 5，5 |
分析 由茎叶图中甲组的数据，根据它们的众数，求出x的值，得出甲组数据的中位数，再求乙组数据的平均数，即得y的值．
解答 解：若甲组数据的众数为124，
则x=4，甲的中位数是：124，
故$\frac{1}{6}$（114+118+122+120+y+127+138）=124，
解得：y=5，
故选：C．
点评 本题考查了茎叶图的应用问题，解题时应根据茎叶图的数据，求出它们的平均数与中位数，从而求出x、y的值．
练习册系列答案
相关题目
14．以$F（0，\frac{p}{2}）（p＞0）$为焦点的抛物线C的准线与双曲线x2-y2=2相交于M，N两点，若△MNF为正三角形，则抛物线C的方程为（ ）
| A． | ${y^2}=2\sqrt{6}x$ | B． | ${y^2}=4\sqrt{6}x$ | C． | ${x^2}=2\sqrt{6}y$ | D． | ${x^2}=4\sqrt{6}y$ |
1．设双曲线$\frac{x^2}{m}+\frac{y^2}{n}=1$的离心率为$\frac{{2\sqrt{3}}}{3}$，且一个焦点与抛物线x2=8y的焦点相同，则此双曲线的方程是（ ）
| A． | $\frac{y^2}{3}-{x^2}=1$ | B． | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | C． | ${y^2}-\frac{x^2}{3}=1$ | D． | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
18．已知集合A={1，3}，$B=\{x|0＜lg（x+1）＜\frac{1}{2}，x∈Z\}$，则A∪B=（ ）
| A． | {1，3} | B． | {1，2，3} | C． | {1，3，4} | D． | {1，2，3，4} |
15．“a＜-1”是“直线ax+y-3=0的倾斜角大于$\frac{π}{4}$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |