题目内容
7．中国宋代的数学家秦九韶曾提出“三斜求积术”，即假设在平面内有一个三角形，边长分别为a，b，c，三角形的面积S可由公式$S=\sqrt{p（p-a）（p-b）（p-c）}$求得，其中p为三角形周长的一半，这个公式也被称为海伦-秦九韶公式，现有一个三角形的边长满足a+b=12，c=8，则此三角形面积的最大值为（ ）| A． | $4\sqrt{5}$ | B． | $8\sqrt{5}$ | C． | $4\sqrt{15}$ | D． | $8\sqrt{15}$ |
分析 由题意，p=10，S=$\sqrt{10（10-a）（10-b）（10-c）}$=$\sqrt{20（10-a）（10-b）}$，利用基本不等式，即可得出结论．
解答 解：由题意，p=10，S=$\sqrt{10（10-a）（10-b）（10-c）}$=$\sqrt{20（10-a）（10-b）}$≤$\sqrt{20}$$•\frac{10-a+10-b}{2}$=8$\sqrt{5}$，
∴此三角形面积的最大值为8$\sqrt{5}$．
故选B．
点评 本题考查面积的计算，考查基本不等式的运用，属于中档题．
练习册系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
16．过直线y=x+1上的点P作圆C：（x-1）2+（y-6）2=2的两条切线l1，l2，当直线l1，l2关于直线y=x+1对称时，|PC|=（ ）
| A． | 3 | B． | 2$\sqrt{2}$ | C． | 1+$\sqrt{2}$ | D． | 2 |
2．如图是由圆柱与两个半球组合而成的几何体的三视图，则该几何体的体积与表面积分别为（ ）
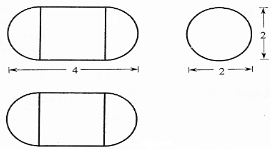
| A． | $\frac{10}{3}π，8π$ | B． | $\frac{16}{3}π，8π$ | C． | $\frac{10}{3}π，10π$ | D． | $\frac{16}{3}π，10π$ |
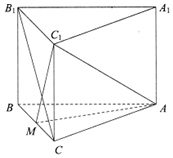在三棱柱ABC-A1B1C1中，已知侧棱CC1⊥底面ABC，M为BC的中点，$AC=AB=3，BC=2，C{C_1}=\sqrt{2}$．