题目内容
已知点P是抛物线x2=4y上一个动点,过点作圆x2+(y-4)2=1的两条切线,切点分别为M,N,则线段MN长度的最小值为 .
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:圆x2+(y-4)2=1的圆心C(0,4),半径r=1.设P(x0,
),可得|PC|=
=
.
利用勾股定理可得|PM|=
=
,利用三角形的面积计算公式可得|MN|=2×
,再利用函数的单调性即可得出.
| ||
| 4 |
|
|
利用勾股定理可得|PM|=
| |PC|2-1 |
|
| |PM||MC| |
| |PC| |
解答:
解:圆x2+(y-4)2=1的圆心C(0,4),半径r=1.
设P(x0,
),
∵|PC|=
=
.
则|PM|=
=
,
∴|MN|=2×
=2
=2
,
当
=8时,|MN|取得最小值=
.
故答案为:
.
设P(x0,
| ||
| 4 |
∵|PC|=
|
|
则|PM|=
| |PC|2-1 |
|
∴|MN|=2×
| |PM||MC| |
| |PC| |
1-
|
1-
|
当
| x | 2 0 |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查了圆的切线的性质、勾股定理、两点之间的距离公式、函数的单调性,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆(x-3)2+(y-4)2=4和直线y=x相交于P,Q两点则|OP|•|OQ|的值是( )
A、
| ||
| B、2 | ||
| C、4 | ||
| D、21 |
如图,在长方形ABCD中,AB=
,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )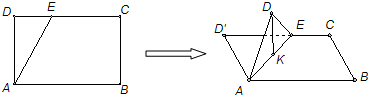
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列1,3,6,10…的一个通项公式是( )
| A、an=n2-(n-1) | ||
B、an=
| ||
| C、an=n2-1 | ||
D、an=
|
用二分法求函数f(x)=ex-4x+1在区间(1,2)内零点的近似值的过程中得到f(15)<0,f(1.75)<0,f(1.875)>0,f(2)>0则函数零点落在区间( )
| A、(1.5,1.75) |
| B、(1.75,1.875) |
| C、(1.875,2) |
| D、不能确定 |
下列命题正确的是( )
| A、若a>b,则ac2>bc2 | ||||
| B、若a2>b2,则a>b | ||||
C、若
| ||||
D、若
|