题目内容
在一个盒子中装有6枝圆珠笔,其中3枝一等品,2枝二等品和1枝三等品,从中任取3枝,求:
(Ⅰ)取出的3枝中恰有1枝一等品的概率;
(Ⅱ)取出的3枝中一、二、三等品各一枝的概率;
(Ⅲ)取出的3枝中没有三等品的概率.
(Ⅰ)取出的3枝中恰有1枝一等品的概率;
(Ⅱ)取出的3枝中一、二、三等品各一枝的概率;
(Ⅲ)取出的3枝中没有三等品的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)恰有一支一等品,从3支一等品中任取一支,从二、三等品种任取两支利用分布乘法原理计算后除以基本事件总数;
(2)恰有一等品、二等品、三等品哥一枝,从一、二、三等品种任取一支利用分布乘法原理计算后除以基本事件总数;
(3)从3支非三等品中任取三支除以基本事件总数.
(2)恰有一等品、二等品、三等品哥一枝,从一、二、三等品种任取一支利用分布乘法原理计算后除以基本事件总数;
(3)从3支非三等品中任取三支除以基本事件总数.
解答:
解:记3枝一等品为A,B,C,2枝二等品为D,E,1枝三等品为F.
从6枝圆珠笔中任取3枝的方法有20种(列举略).
(Ⅰ)取出的3枝中恰有1枝一等品的方法有9种(列举略),所以,所求概率p1=
.…(4分)
(Ⅱ)取出的3枝中一、二、三等品各一枝的概率的方法有6种(列举略),所以,所求概率p2=
…(8分)
(Ⅲ)取出的3枝中没有三等品的方法有10种(列举略),所以,所求
概率p3=
.…(12分)
从6枝圆珠笔中任取3枝的方法有20种(列举略).
(Ⅰ)取出的3枝中恰有1枝一等品的方法有9种(列举略),所以,所求概率p1=
| 9 |
| 20 |
(Ⅱ)取出的3枝中一、二、三等品各一枝的概率的方法有6种(列举略),所以,所求概率p2=
| 3 |
| 10 |
(Ⅲ)取出的3枝中没有三等品的方法有10种(列举略),所以,所求
概率p3=
| 1 |
| 2 |
点评:本题主要考查古典概型,可用列举法一一列举,也可以用排列组合进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知某几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
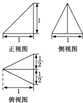

A、
| ||
B、
| ||
C、
| ||
D、
|
设x,y满足的条件
若z=x+3y+m的最小值为4,则m=( )
|
| A、1 | B、2 | C、3 | D、4 |
若不等式组
表示的平面区域是一个三角形,则s的取值范围是( )
|
| A、0<s≤2或s≥4 |
| B、0<s≤2 |
| C、2≤s≤4 |
| D、s≥4 |
设函数f(x)=
,则f[f(4)]=( )
|
| A、2 | B、4 | C、8 | D、16 |