题目内容

10．解不等式组：$\left\{\begin{array}{l}{\frac{2}{x-2}＜-1}\\{1＜|x|＜3}\end{array}\right.$．

分析 由条件利用分式不等式、绝对值不等式的解法，等价转化，求得x的范围．

解答 解：不等式组 $\left\{\begin{array}{l}{\frac{2}{x-2}＜-1}\\{1＜|x|＜3}\end{array}\right.$，即 $\left\{\begin{array}{l}{\frac{x}{x-2}＜0}\\{1＜x＜3或-3＜x＜-1}\end{array}\right.$，即 $\left\{\begin{array}{l}{x（x-2）＜0}\\{1＜x＜3或-3＜x＜-1}\end{array}\right.$，
求得 1＜x＜2，即原不等式组的解集为（1，2）．

点评 本题主要考查分式不等式、绝对值不等式的解法，体现了转化的数学思想，属于基础题．

练习册系列答案
相关题目
20．已知全集U=R，A={x|-1≤x≤3}，B={x|x-a≥0}．
（Ⅰ）当a=2时，求A∪B，A∩∁UB；
（Ⅱ）若0∈A∩B，求a的取值范围．（写出解答过程）
1．设a、b为两条不同的直线，α、β为两个不同的平面，则下列命题中为真命题的是（　　）
A．若a⊥α，α⊥β，则a∥βB．若a∥α，b∥α，则a∥bC．若a∥α，α⊥β，则a⊥βD．若a⊥α，a∥β，则α⊥β
18．已知抛物线的方程为y2=8x，过其焦点F的直线l与抛物线交于A、B两点，若S△AOF=S△BOF（O为坐标原点），则|AB|=（　　）
A．$\frac{16}{3}$B．8C．$\frac{4}{3}$D．4
5．设常数a∈（0，1），已知f（x）=loga（x2-2x+6）是区间（m，m+$\frac{5}{2}$）上的增函数，则最大负整数m的值为-2．
15．截至11月27日，国内某球员在2015-2016赛季CBA联赛的前10轮比赛中，各场得分xi（i=1，2，3，…，10）的茎叶图如图①所示，图②是该运动员某项成绩指标分析的程序框图，则输出的结果是（　　）
A．8B．7C．6D．5
2．一个三棱锥的三视图如图所示，则它的体积为（　　）
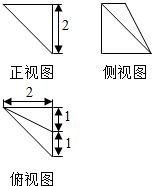
A．$\frac{2}{3}$B．1C．$\frac{4}{3}$D．2
19．$\overrightarrow{a}$，$\overrightarrow{b}$为单位向量，且|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{7}$，则向量$\overrightarrow{a}$，$\overrightarrow{b}$夹角为（　　）
A．30°B．45°C．60°D．90°
20．若三个正数a，b，c成等比数列，其中a=5+2$\sqrt{3}$，c=5-2$\sqrt{3}$，则b=$\sqrt{13}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网