题目内容
5.设常数a∈(0,1),已知f(x)=loga(x2-2x+6)是区间(m,m+$\frac{5}{2}$)上的增函数,则最大负整数m的值为-2.分析 根据对数函数的单调性结合函数单调性的关系,转化为一元二次函数的性质,进行求解即可.
解答 解:设t=x2-2x+6,则t=(x-1)2+5>0,则函数的定义域为(-∞,+∞),
∵a∈(0,1),
∴y=logat为增函数,
若f(x)=loga(x2-2x+6)是区间(m,m+$\frac{5}{2}$)上的增函数,
则等价为t=x2-2x+6是区间(m,m+$\frac{5}{2}$)上的减函数,
则m+$\frac{5}{2}$≤1,
即m≤1-$\frac{5}{2}$=-$\frac{3}{2}$,
∵m是整数,
∴最大的整数m=-2,
故答案为:-2
点评 本题主要考查复合函数单调性的应用,利用换元法,转化为一元二次函数是解决本题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
15.如图,正方体中,两条异面直线BC1与B1D1所成的角是( )
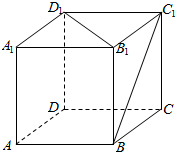

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
17.某中学高一、高二各有一个文科和一个理科两个实验班,现将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学,每个班级去一所高校,每所高校至少有一个班级去,则恰好有一个文科班和一个理科班分配到上海交通大学的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
15.已知Sn为等差数列{an}的前n项和,若a5=7,则S9=( )
| A. | 45 | B. | 53 | C. | 63 | D. | 72 |