题目内容
20.已知全集U=R,A={x|-1≤x≤3},B={x|x-a≥0}.(Ⅰ)当a=2时,求A∪B,A∩∁UB;
(Ⅱ)若0∈A∩B,求a的取值范围.(写出解答过程)
分析 (Ⅰ)根据交集、并集与补集的定义,进行运算即可;
(Ⅱ)讨论a的值,求出满足0∈A∩B时a的取值范围.
解答 解:(Ⅰ)当a=2时,B={x|x≥2},
所以A∪B={x|x≥-1};…(2分)
因为∁UB={x|x<2},…(4分)
所以A∩(∁UB)={x|-1≤x<2};…(6分)
(Ⅱ)当a≤-1时,A∩B={x|-1≤x≤3},0∈A∩B;…(7分)
当-1<a<3时,A∩B={x|a≤x≤3},…(8分)
要使0∈A∩B,只需-1<a≤0;…(9分)
当a=3时,A∩B={3},
此时,0∉A∩B;
当a>3时,A∩B=ϕ,…(10分)
此时,0∉A∩B;…(11分)
综上所述,当a≤0时,0∈A∩B.…(12分)
点评 本题考查了集合的定义与运算问题,也考查了分类讨论思想的应用问题,是基础题目.

练习册系列答案
相关题目
15.如图,正方体中,两条异面直线BC1与B1D1所成的角是( )
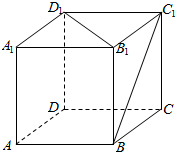

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
12.与函数y=|x|相等的函数是( )
| A. | y=($\sqrt{x}$)2 | B. | y=($\root{3}{x}$)3 | C. | y=$\sqrt{{x}^{2}}$ | D. | y=$\root{3}{{x}^{3}}$ |
