题目内容
已知不等式
<0的解集为M,若2∉M,则a的取值范围是 .
| ax2+2x-3 |
| ax-1 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:根据元素和集合之间的关系,结论不等式的解法即可得到结论.
解答:
解:∵2∉M,
当x=2时,分母2a-1=0,或者
≥0,
即a=
或
≥0,
即(4a+1)(2a-1)≥0,
解得a≥
或a≤-
,
故答案为:{a|a≥
或a≤-
}.
当x=2时,分母2a-1=0,或者
| 4a+4-3 |
| 2a-1 |
即a=
| 1 |
| 2 |
| 4a+1 |
| 2a-1 |
即(4a+1)(2a-1)≥0,
解得a≥
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:{a|a≥
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题主要考查不等式的解法,利用元素和集合之间的关系,转化为不等式关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
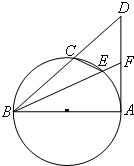 如图,BA是圆O的直径,C、E在圆0上,BC、BE的延长线交直线AD于点D、F,BA2=BC•BD.求证:
如图,BA是圆O的直径,C、E在圆0上,BC、BE的延长线交直线AD于点D、F,BA2=BC•BD.求证: