题目内容
求函数f(x)=2x2-x+3+
的最小值 .
| x2-x |
考点:函数的最值及其几何意义
专题:计算题,导数的综合应用
分析:先求函数f(x)=2x2-x+3+
的定义域为(-∞,0]∪[1,+∞);再求导f′(x)=4x-1+
;从而由导数确定函数的单调性及最小值.
| x2-x |
| 2x-1 | ||
2
|
解答:
解:函数f(x)=2x2-x+3+
的定义域为(-∞,0]∪[1,+∞);
f′(x)=4x-1+
;
故当x∈(-∞,0)时,f′(x)<0;
当x∈(1,+∞)时,f′(x)>0;
故函数f(x)=2x2-x+3+
在(-∞,0]上是减函数,
在[1,+∞)上是增函数;
当x∈(-∞,0]时,fmin(x)=3;
当x∈[1,+∞)时,fmin(x)=4;
故答案为:3.
| x2-x |
f′(x)=4x-1+
| 2x-1 | ||
2
|
故当x∈(-∞,0)时,f′(x)<0;
当x∈(1,+∞)时,f′(x)>0;
故函数f(x)=2x2-x+3+
| x2-x |
在[1,+∞)上是增函数;
当x∈(-∞,0]时,fmin(x)=3;
当x∈[1,+∞)时,fmin(x)=4;
故答案为:3.
点评:本题考查了导数的综合应用及函数的最值问题,属于中档题.

练习册系列答案
相关题目
下列曲线中离心率为
的是( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某四棱锥的三视图如图所示,则该四棱锥的体积为( )


| A、2 | B、4 | C、8 | D、12 |
化简:(sin
+cos
)2+2sin2(
-
)得( )
| α |
| 2 |
| α |
| 2 |
| π |
| 4 |
| α |
| 2 |
| A、2+sinα | ||||
B、2+
| ||||
| C、2 | ||||
D、2+
|
某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
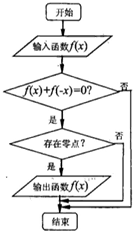

| A、f(x)=cosx | ||
B、f(x)=
| ||
| C、f(x)=lgx | ||
D、f(x)=
|
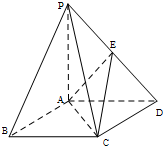 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.