题目内容
用cosα表示sin4α-sin2α+cos2α.
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:直接利用三角函数的平方关系化简求值.
解答:
解:sin4α-sin2α+cos2α
=sin2α(sin2α-1)+cos2α
=(1-cos2α)(-cos2α)+cos2α
=-cos2α+cos4α+cos2α
=cos4α.
=sin2α(sin2α-1)+cos2α
=(1-cos2α)(-cos2α)+cos2α
=-cos2α+cos4α+cos2α
=cos4α.
点评:本题考查了同角三角函数的基本关系式,是基础题.

练习册系列答案
相关题目
在下列四个命题中,其中正确命题的是( )
| A、有两个面互相平行,其余各面都是平行四边形的多面体是棱柱 |
| B、有一个面是多边形,其余各面都是三角形的几何体叫棱锥 |
| C、有两个面互相平行,其余各面都是梯形的多面体是棱台 |
| D、用平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台 |
 若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积等于( )
若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积等于( )| A、12πcm2 |
| B、15πcm2 |
| C、24πcm2 |
| D、30πcm2 |
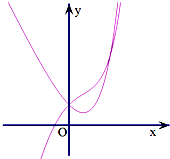 已知函数f(x)=ex-x2的导函数为f′(x),y=f(x)与y=f′(x)在同一直角坐标系下的部分图象如图所示,若方程f′(x)-f(a)=0在x∈(-∞,a]上有两解,则实数a的取值范围是
已知函数f(x)=ex-x2的导函数为f′(x),y=f(x)与y=f′(x)在同一直角坐标系下的部分图象如图所示,若方程f′(x)-f(a)=0在x∈(-∞,a]上有两解,则实数a的取值范围是