题目内容
化简：a2+b2-2ab-c2= ．
考点：因式分解定理
专题：函数的性质及应用
分析：直接利用平方差法分解因式即可．
解答：
解：a2+b2-2ab-c2=（a-b）2-c2=（a-b+c）（a-b-c）．
故答案为：（a-b+c）（a-b-c）．
故答案为：（a-b+c）（a-b-c）．
点评：本题考查因式分解定理的应用，基本知识的考查．
练习册系列答案
相关题目
设集合A={x|-2＜x＜3}，B={x|x≤1或x≥4}．若全集U=R，则A∩∁UB=（ ）
| A、{x|1＜x≤3} |
| B、{x|1＜x＜3} |
| C、{x|1≤x＜3} |
| D、{x|x≤1或x≥3} |
关于直线l，m与平面α，β的命题中，一定正确的是（ ）
| A、若l∥m，m?α，则l∥α |
| B、若l⊥β，α⊥β，则l∥α |
| C、若l⊥β，α∥β，则l⊥α |
| D、若l?β，α⊥β，则l⊥α |
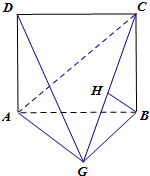已知四棱锥G-ABCD，四边形ABCD是长为2a的正方形，DA⊥平面ABG，且GA=GB，BH⊥平面CAG，垂足为H，且H在直线CG上．