题目内容
4.已知f(x)=$\frac{{{e^{-x}}}}{a}+\frac{a}{{{e^{-x}}}}$(a>0)是定义在R上的偶函数,(1)求实数a的值;
(2)判断并证明函数f(x)在[0,+∞)的单调性;
(3)若关于x的不等式f(x)-m2+m≥0的解集为R,求实数m的取值范围.
分析 (1)根据函数奇偶性的定义建立方程关系进行求解即可.
(2)根据函数单调性的定义进行判断和证明.
(3)根据函数单调性的性质,利用参数分离法进行求解即可.
解答 解:(1)∵f(x)为偶函数,∴f(-x)=f(x)
即$\frac{{e}^{x}}{a}$+$\frac{a}{{e}^{x}}$=$\frac{{{e^{-x}}}}{a}+\frac{a}{{{e^{-x}}}}$.
∴$\frac{{e}^{x}-{e}^{-x}}{a}$=a(ex-e-x),
∵(ex-e-x)≠0,
∴a=$\frac{1}{a}$,即a=±1.
而a>0,∴a=1,∴f(x)=ex+e-x.…(4分)
(2)函数f(x)在[0,+∞)上是单调递增的.
证明:任取x1,x2∈[0,+∞)且x1<x2,
则f(x1)-f(x2)=${e}^{{x}_{1}}$+${e}^{-{x}_{1}}$-${e}^{{x}_{2}}$-${e}^{-{x}_{2}}$=(${e}^{{x}_{1}}$-${e}^{{x}_{2}}$)•$\frac{{e}^{{x}_{1}}{e}^{{x}_{2}}-1}{{e}^{{x}_{1}}{e}^{{x}_{2}}}$,
∵x1,x2∈[0,+∞)且x1<x2,
∴${e}^{{x}_{1}}$-${e}^{{x}_{2}}$<0•${e}^{{x}_{1}}$${e}^{{x}_{2}}$>1•
∴(${e}^{{x}_{1}}$-${e}^{{x}_{2}}$)•$\frac{{e}^{{x}_{1}}{e}^{{x}_{2}}-1}{{e}^{{x}_{1}}{e}^{{x}_{2}}}$<0,
即f(x1)<f(x2),
∴f(x)在[0,+∞)上是增函数. …(9分)
(3)由题意,m2-m≤f(x)在x∈R上恒成立,
则只需m2-m≤fmin(x)
∵f(x)为偶函数,且f(x)在[0,+∞)上是增函数,
∴f(x)在(-∞,0)上是减函数,
∴f(x)的最小值为fmin(x)=f(0)=2
则有m2-m≤2,
因此m∈[-1,2]. …(12分)
点评 本题主要考查函数恒成立问题以及函数奇偶性和单调性的判断和应用,利用定义法以及转化法是解决本题的关键.综合考查函数的性质.

 阅读快车系列答案
阅读快车系列答案 函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )| A. | 函数f(x)的最小正周期为8 | |
| B. | f(3)=-$\frac{1}{2}$ | |
| C. | x=-1是函数f(x)的一条对称轴 | |
| D. | 函数f(x)向左平移一个单位长度后所得的函数为偶函数 |
| A. | $(-1,\frac{π}{2})$ | B. | $(\frac{π}{3}-1,\frac{π}{3})$ | C. | $(\frac{π}{3}-1,\frac{π}{3}+1)$ | D. | $(\frac{π}{6},\frac{π}{6}+1)$ |
| A. | a<b<c | B. | b<c<a | C. | b<a<c | D. | c<b<a |
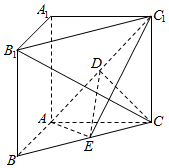 如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.
如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.