题目内容
13.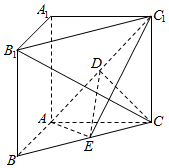 如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.
如图,在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC的中点,D是AC1中点.(1)求证:B1C⊥平面AEC1;
(2)求三棱锥C-AED的体积.
分析 (1)证明AE⊥B1C,B1C⊥EC1,即可证明B1C⊥平面AEC1;
(2)利用等体积转换,即可求三棱锥C-AED的体积.
解答 (1)证明:∵AB=AC,E是BC的中点,
∴AE⊥平面B1C.
∵B1C?平面B1C,
∴AE⊥B1C.
∵CC1⊥平面ABC,∠BAC=90°,AB=AC=AA1=2,
∴$\frac{CE}{{B}_{1}B}$=$\frac{{C}_{1}C}{BC}$=$\frac{\sqrt{2}}{2}$,
∴△C1CE∽△CBB1,
∴∠B1CB=∠CC1E,
∴B1C⊥EC1,
∵EC1∩AE=E,
∴B1C⊥平面AEC1;
(2)解:三棱锥C-AED的体积=$\frac{1}{2}$×三棱锥C1-AED的体积=$\frac{1}{2}×\frac{1}{3}×\frac{1}{2}×\frac{1}{2}×2×2×2$=$\frac{1}{3}$.
点评 本题考查线面垂直的判定,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
8.已知三棱柱ABC-A1B1C1的侧棱和底面垂直,底面是正三角形,侧棱长是底边长的2倍,若该三棱柱的各顶点都在球O的表面上,且球O的表面积为36π,则此三棱锥A-A1B1C1的体积为( )
| A. | $\frac{121}{25}$ | B. | $\frac{81}{16}$ | C. | $\frac{16}{9}$ | D. | $\frac{9}{4}$ |
 如图所示的几何体中,四边形ABCD和四边形BCEF是全等的等腰梯形,且平面BCEF⊥平面ABCD,AB∥DC,CE∥BF,AD=BC,AB=2CD,∠ABC=∠CBF=60°,G为线段AB的中点
如图所示的几何体中,四边形ABCD和四边形BCEF是全等的等腰梯形,且平面BCEF⊥平面ABCD,AB∥DC,CE∥BF,AD=BC,AB=2CD,∠ABC=∠CBF=60°,G为线段AB的中点