题目内容
11．
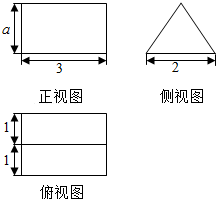如图是一个几何体的三视图，若它的体积是3$\sqrt{3}$，则a=$\sqrt{3}$，该几何体的表面积为2$\sqrt{3}$+18．
分析 根据几何体的三视图，得出该几何体是一平放的三棱柱，由体积求出a的值，再求它的表面积．
解答 解：根据几何体的三视图，得；
该几何体是一平放的三棱柱，
且三棱柱的高是3，底面三角形的边长为2，高为a；
∴该三棱柱的体积为
V=$\frac{1}{2}$×2×a×3=3$\sqrt{3}$，
解得a=$\sqrt{3}$；
∴该三棱柱的表面积为：
S=2S△+3S侧面=2×$\frac{1}{2}$×2×$\sqrt{3}$+3×3×$\sqrt{{1}^{2}{+（\sqrt{3}）}^{2}}$=2$\sqrt{3}$+18．
故答案为：$\sqrt{3}$，2$\sqrt{3}$+18．
点评 本题考查了利用几何体的三视图求体积与表面积的应用问题，是基础题目．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
16．动圆P和圆C1：（x+1）2+y2=$\frac{1}{4}$外切和圆C2：（x-2）2+y2=$\frac{49}{4}$内切，那么动圆圆心P和已知两圆的圆心C1、C2构成三角形PC1C2的周长等于（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
3．若先将函数y=sin（4x+$\frac{π}{6}$）图象上各点的纵坐标不变，横坐标伸长到原来的2倍，再将所得图象向左平移$\frac{π}{6}$个单位，则所得函数图象的一条对称轴的方程是（ ）
| A． | x=$\frac{π}{12}$ | B． | x=$\frac{π}{6}$ | C． | x=$\frac{π}{3}$ | D． | x=$\frac{π}{2}$ |