题目内容
已知函数f（x）=lnx-ax2（a∈R），求函数f（x）的单调区间．
考点：函数的单调性及单调区间
专题：导数的综合应用
分析：求函数的定义域，利用函数单调性和导数之间的关系即可求出函数的单调区间．
解答：
解：要使函数有意义，则x＞0，
函数的导数f′(x)=
-2ax=
，
若a≤0，则f'（x）＞0，此时函数单调递增，即增区间为（0，+∞）．
若a＞0，由f′（x）＞0得0＜x＜
，
由f′（x）＜0得x＞
，即此时函数的增区间为（0，
），减区间为（
，+∞），
综上：若a≤0，函数的增区间为（0，+∞）．
若a＞0，函数的增区间为（0，
），减区间为（
，+∞）．
函数的导数f′(x)=
| 1 |
| x |
| 1-2ax2 |
| x |
若a≤0，则f'（x）＞0，此时函数单调递增，即增区间为（0，+∞）．
若a＞0，由f′（x）＞0得0＜x＜
| 1 | ||
|
由f′（x）＜0得x＞
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
综上：若a≤0，函数的增区间为（0，+∞）．
若a＞0，函数的增区间为（0，
| 1 | ||
|
| 1 | ||
|
点评：本题主要考查函数单调区间的求解，利用函数单调性和导数之间的关系，即可得到结论，注意要对参数进行讨论．
练习册系列答案
相关题目
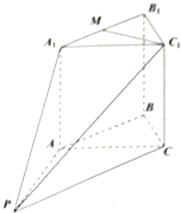如图所示，在正三棱柱（底面是正三角形的直棱柱）A1B1C1-ABC中，M为A1B1的中点，P∈平面ABC，PA⊥平面ACC1A1，且AB=AA1=4，PA=4
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直，AB=2AD=2CD=4，∠ABE=60°，∠BAD=∠CDA=90°，点H、G分别是线段EF、BC的中点．