题目内容

设等比数列{an}的前n项积Pn=a1•a2•a3•…•an，若P12=32P7，则a10等于（　　）
A、16B、8C、4D、2
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：利用P12=32P7，求出a8•a9•…•a12=32，再利用等比数列的性质，可求a10．
解答： 解：由题意，∵P12=32P7，
∴a1•a2•a3•…•a12=32a1•a2•a3•…•a7，
∴a8•a9•…•a12=32，
∴（a10）5=32，
∴a10=2．
故选：D．
点评：本题考查等比数列{an}的前n项积，考查等比数列的性质，属于基础题．
练习册系列答案
相关题目
执行如图所示算法的伪代码，则输出S的值为
 
．
已知函数f（x-2）=
1+2x2，x＞2
2x，x≤2
，则f（1）=
 
．
若函数f（x）满足：f（x）-4f（
1
x
）=x，则|f（x）|的最小值为（　　）
A、
2
15
B、
4
15
C、
2
15
15
D、
4
15
15
设函数f（x）的定义域为D，如果?x∈D，?y∈D，使得f（x）=-f（y）成立，则称函数f（x）为“Ω函数”．给出下列四个函数：
①y=sinx；
②y=2x；
③y=
1
x-1
；
④f（x）=lnx，
则其中“Ω函数”共有（　　）
A、1个B、2个C、3个D、4个
设i为虚数单位，则
-2i
1-i
等于（　　）
A、1-iB、1+i
C、-1+iD、-1-i
一几何体的三视图如图，该几何体的顶点都在球O的球面上，球O的表面积是（　　）
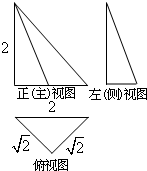
A、2πB、4πC、8πD、16π
若实数（x，y）满足条件
x+2y≤4
2x+y≤4
x≥0
y≥0
，则z=
x2+(y+1)2
的最大值为（　　）
A、
3
B、
65
3
C、
65
9
D、3
在星期一至星期五的5天内安排语、数、英三科测试，每天最多进行一门考试，且语文和数学不能连续两天考试，那么不同的考试安排方案种数共有（　　）
A、18B、36C、12D、48

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网