题目内容
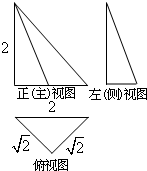
一几何体的三视图如图,该几何体的顶点都在球O的球面上,球O的表面积是( )

| A、2π | B、4π | C、8π | D、16π |
考点:由三视图求面积、体积
专题:空间位置关系与距离,球
分析:几何体为三棱锥,且三棱锥的一条侧棱与底面垂直,底面为等腰直角三角形,取O为SC的中点,可证OS=OC=OA=OB,由此求得外接球的半径,代入球的表面积公式计算.
解答:
解:由三视图知:几何体为三棱锥,且三棱锥的一条侧棱与底面垂直,高为2,
底面为等腰直角三角形,如图:SA⊥平面ABC,SA=2,AC的中点为D,
在等腰直角三角形SAC中,取O为SC的中点,∴OS=OC=OA=OB,
∴O为三棱锥外接球的球心,R=
,
∴外接球的表面积S=4π×(
)2=8π.
故选:C.
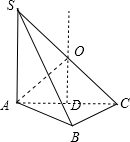
底面为等腰直角三角形,如图:SA⊥平面ABC,SA=2,AC的中点为D,
在等腰直角三角形SAC中,取O为SC的中点,∴OS=OC=OA=OB,
∴O为三棱锥外接球的球心,R=
| 2 |
∴外接球的表面积S=4π×(
| 2 |
故选:C.

点评:本题考查了由三视图求几何体的外接球的表面积,判断几何体的特征性质及数据所对应的几何量是关键.

练习册系列答案
相关题目
设等比数列{an}的前n项积Pn=a1•a2•a3•…•an,若P12=32P7,则a10等于( )
| A、16 | B、8 | C、4 | D、2 |
设a=(
) log23,b=(
) log54,c=3ln3,则a,b,c的大小关系是( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、c>a>b |
| B、c>b>a |
| C、a>b>c |
| D、a>c>b |
已知a∈R,i是虚数单位,z=2+(2-a)i∈R,在复平面内,复数a-zi对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下面是一个2×2列联表:
则表中a,b的值分别为( )
| y1 | y2 | 合计 | |
| x1 | a | c | 73 |
| x2 | 22 | 25 | 47 |
| 合计 | b | 46 | 120 |
| A、94,72 |
| B、52,50 |
| C、52,74 |
| D、74,52 |