题目内容
若函数y=sinωx在(-
,
)内是增函数,则ω的取值范围为 .
| π |
| 2 |
| π |
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据正弦函数的单调性进行求解即可.
解答:
解:∵函数y=sinωx在(-
,
)内是增函数,
∴ω>0且
≥
,
即T≥2π,
∴
≥2π,
即0<ω≤1,
故答案为:0<ω≤1
| π |
| 2 |
| π |
| 2 |
∴ω>0且
| T |
| 4 |
| π |
| 2 |
即T≥2π,
∴
| 2π |
| ω |
即0<ω≤1,
故答案为:0<ω≤1
点评:本题主要考查三角函数单调性的应用,根据正弦函数的单调性是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=lnx+x2-3x,则其导函数f′(x)的图象与x轴所围成的封闭图形的面积为( )
| A、ln2 | ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=sinx+cosx,x∈R,则下列结论正确的是( )
| A、f(x)是奇函数 | ||
| B、f(x)的值域为[-2,2] | ||
C、f(x)关于点(-
| ||
D、f(x)有一条对称轴为x=
|
函数f(x)的导函数f′(x)的图象如图所示,则下列说法正确的是( )
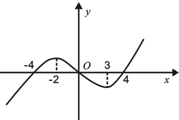

| A、函数f(x)在(-2,3)内单调递减 |
| B、函数f(x)在x=3处取极小值 |
| C、函数f(x)在(-4,0)内单调递增 |
| D、函数f(x)在x=4处取极大值 |
已知等比数列{an}是递增数列,Sn是数列{an}的前n项和,若a1,a3是方程x2-5x+4=0的两个根,则S5等于( )
| A、15 | B、31 | C、32 | D、51 |