题目内容
已知函数f(x)=sin2x(x∈R),为了得到函数g(x)=sin(2x+
)的图象,只要将y=f(x)的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:化简两个函数式之间的关系,根据三角函数的平移关系即可得到结论.
解答:
解:∵g(x)=sin(2x+
)=sin[2(x+
)],
∴y=f(x)的图象向左平移
个单位长度,即可得到函数g(x)=sin(2x+
)的图象,
故选:A
| π |
| 4 |
| π |
| 8 |
∴y=f(x)的图象向左平移
| π |
| 8 |
| π |
| 4 |
故选:A
点评:本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律.

练习册系列答案
相关题目
函数f(x)的导函数f′(x)的图象如图所示,则下列说法正确的是( )
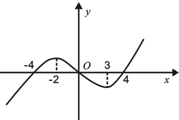

| A、函数f(x)在(-2,3)内单调递减 |
| B、函数f(x)在x=3处取极小值 |
| C、函数f(x)在(-4,0)内单调递增 |
| D、函数f(x)在x=4处取极大值 |
若函数f(x)=3x,它的反函数是g(x),a=g(3),b=g(4),c=g(π),则下面关系式中正确的是( )
| A、a<b<c |
| B、a<c<b |
| C、b<c<a |
| D、b<a<c |
下列结论正确的是( )
A、x>1⇒
| ||||
B、x+
| ||||
C、x>y⇒
| ||||
| D、x>y⇒x2>y2 |
命题“若a2>b2,则a>b”的否命题是( )
| A、若a2≤b2则,则a>b |
| B、若a2<b2,则a<b |
| C、若a2≤b2则,则a≤b |
| D、若a2<b2,则a>b |
已知等比数列{an}是递增数列,Sn是数列{an}的前n项和,若a1,a3是方程x2-5x+4=0的两个根,则S5等于( )
| A、15 | B、31 | C、32 | D、51 |
已知直线l:y=x与圆C:(x-a)2+y2=1,则“a=
”是“直线l与圆C相切”的( )
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |